Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 6

Суммируемый ряд может содержать символьные компоненты, например, такие, как в следующем выражении:    .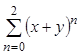

Командная строка для этого случая должна иметь такой вид:

¤((x + y)^n, n, 0, 2)

а будучи выведенной на поле алгебры – следующий:

 2         n

 ¤  (x + y)

n=0         

После выделения этого выражения курсором и нажатии клавиши ═, будет выведен следующий результ:

 2                  2        

x  + x·(2·y + 1) + y  + y + 1

В выражения n-го члена ряда и пределы суммирования могут входить и векторы, и матрицы, и различные операторы. Например, пусть задана матрица М заранее неизвестной размерности и необходимо найти сумму ее строк, начиная со строки, номер которой стоит во второй строке и третьем столбце, и кончая последней строкой матрицы. Математически это можно записать так 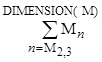  .   Первый индекс у векторов всегда единица.

Пусть для примера определена или получена ранее следующая матрица:

M := [[1, 2, 3], [2, -1, 1], [2, 3, -2]]

     „ 1   2   3 †

     ¦           ¦

M := ¦ 2  -1   1 ¦

     ¦           ¦

     … 2   3  -2 ‡

В командной строке наберем следующий текст:

¤(M™n, n, M™2™3, DIMENSION(M))

Этот текст на поле алгебраического окна выведет следующее выражение:

DIMENSION(M)   

     ¤       M

  n=M™2™3     n

После выделения этого выражения курсором и нажатия «горячей» клавиши  ═  получим результирующий вектор, как сумму трех строк:

[5, 4, 2]

В последних выражениях встроенный оператор DIMENSION(M) возвращает размерность вектора с векторными компонентами. В данном случае это число строк. 

Значения пределов могут быть получены вычислением из любого выражения, однако их конечное значение должно быть только целым. Действительное число может быть превращено в целое встроенным оператором FLOOR(), аргументом которого может быть любая функция, возвращающая действительное число

FLOOR(7.645)                                               Þ 7

FLOOR(7.445+ 1/2)                                        Þ 7

FLOOR(7.645 + 1/2)                                       Þ 8

Первая строка выделяет целую часть действительного числа путем отбрасывания дробной части, а две следующие – округляют действительные числа до ближайших целых. Такое округление обычно называют правильным.

Вычисление произведения членов ряда

Вычисление произведения членов ряда во всем похожи на вычисление суммы. Отличие лишь в том, что запись в командной строке и изображение произведения в алгебраическом окне вместо знака  Σ  содержат греческую букву верхнего регистра  £. Например, для вычисления произведения всех элементов третьей колонки матрицы M, приведенной выше, в командной строке набрать следующий текст:

£(M™n™3, n, 1, DIMENSION(M))

Вид набранного выражения в алгебраическом окне будет таким

DIMENSION(M)     

     £       M                      Þ   -6

    n=1       n,3

Конкретное значение результата показано справа.

Разрешено вложение циклических операторов суммирования и умножения друг в друга любой глубины. Развертка этих циклов при вычислениях начинается с самого глубокого. Для примера выполнения вложенных циклов рассмотрим вычисление произведения всех элементов матрицы M. Запись в командной строке, изображение команды на экране и результат вычислений будут иметь следующий вид:

£(£(M™n™m, n, 1, DIMENSION(M)), m, 1, DIMENSION(M))

DIMENSION(M) DIMENSION(M)     

     £            £       M              Þ   144

    m=1          n=1       n,m

или иначе, с применением оператора присваивания, если некоторые фрагменты повторяются много раз, как в предыдущем примере,

£(£(M™n™m, n, 1, j := DIMENSION(M)), m, 1, j)

 j  j := DIMENSION(M)     

 £          £         M                  Þ   144

m=1        n=1         n,m

Для этого и других подобных случаев следует помнить, что, где бы ни был вставлен оператор присваивания, имя левой части получает соответствующее значение и оказывается доступным при вызове этой переменной по имени в любых выражениях текущего сеанса до тех пор, пока другим оператором присваивания это значение не будет изменено. После выполнения рассмотренного примера переменная j будет иметь значение, равное 3.