Информатика и выч. техника \ Программирование

Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 32

…        i+1              ‡

„        t0=1        †

¦        t1=x        ¦

¦            2       ¦

¦      t2=2·x -1     ¦

¦           3        ¦

¦     t3=4·x -3·x    ¦

¦         4    2     ¦

¦   t4=8·x -8·x +1   ¦

¦        5     3     ¦

… t5=16·x -20·x +5·x ‡

Чтобы разрешить эту систему уравнений относительно степеней xi, заменим последние на простые переменные    x0,..., x5 и применим оператор SOLVE() :

     €„        t0=x0        † „ x0 †‚

     ¦¦        t1=x1        ¦ ¦ x1 ¦¦

SOLVE¦¦     t2=2·x2-x0      ¦,¦ x2 ¦¦`

     ¦¦    t3=4·x3-3·x1     ¦ ¦ x3 ¦¦

     ¦¦   t4=8·x4-8·x2+x0   ¦ ¦ x4 ¦¦

     … t5=16·x5-20·x3+5·x1 ‡ … x5 ‡ƒ

„        x0=t0       †

¦        x1=t1       ¦

¦         t0+t2      ¦

¦     x2=——————-     ¦

¦           2        ¦

¦        3·t1+t3     ¦

¦    x3=————————-    ¦

¦           4        ¦

¦      3·t0+4·t2+t4  ¦

¦  x4=—————————————- ¦

¦            8       ¦

¦     10·t1+5·t3+t5  ¦

¦ x5=——————————————- ¦

…           16       ‡

Полученные выражения для степеней x подставим теперь в степенной многочлен G(x) из задачи №3, раскроем скобки и приведем подобные:

              10·t1+5·t3+t5           4·t2+t4+3·t0

Gti=0.248628·——————————————--2.72847·—————————————- +

                    16                      8      

         3·t1+t3           t2+t0                       

+11.5865·————————--24.1605·——————-+24.1524·t1-8.4889·t0

            4                2                         

После приведения получим

Gti=-21.59235625·t0+32.9976675·t1-13.444485·t2+

+2.97432125·t3-0.34105875·t4+0.01553925·t5

Для проверки подставим x=1 в многочлены Gti и G(x) :

lim „VECTOR(t   =T(x,i),i,0,5)†

x˜1 …        i+1              ‡

[ t0=1  t1=1  t2=1  t3=1  t4=1  t5=1 ]

-21.59235625+32.9976675-13.444485+2.97432125-0.34105875+0.01553925

0.609628

          5          4          3          2                  

0.248628·1 -2.72847·1 +11.5865·1 -24.1605·1 +24.1524·1-8.48893

0.609628

Задача №16: Уравнение теплопроводности

Выравнивание температуры T(x,t) на однородном теплоизолированном стержне описывается дифференциальным уравнением в частных производных

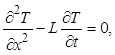
с начальным распределением температуры по длине стержня в шести равномерно расположенных с шагом  h  внутренних точках.

 

На концах стержня в точках  и  удерживается нулевая температура.

Применяя конечно-разностное представление производных по пространственной переменной x, свести уравнение в частных производных к системе дифференциальных уравнений в обыкновенных производных.

Теоретические предпосылки аппроксимации уравнения

Заданное уравнение в частных производных устанавливает дифференциальную зависимость между физическими (размерными) величинами: длиной, температурой, временем и свойствами материала. Поэтому исходное уравнение приведем к каноническому виду, в котором размерные переменные заменим безразмерными следующей подстановкой:

,       .

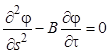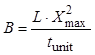Коэффициент , описывающий свойства материала стержня, включает в себя коэффициент теплопроводности 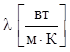, удельную теплоемкость 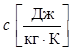 и плотность .

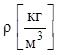Для аппроксимации производных конечными разностями необходимо выбрать количество точек, по значениям функции в которых вычисляться производные. От количества точек аппроксимации зависит точность воспроизведения кривых переходного процесса, то есть его динамики. Грубо говоря, количество точек, вовлеченное в вычисление, определяет локальную степень многочлена, проходящего через выбранные точки. Чем степень меньше, тем большее число точек необходимо брать на заданной длине, чтобы более точно вычислить кривые переходных процессов. В данной задаче общее число точек задано, поэтому для повышения точности желательно выбирать многоточечную аппроксимацию.

В рассматриваемом примере применим 5-точечную аппроксимацию для пространственной переменной s, а временную переменную оставим непрерывной, заменив в аппроксимирующих уравнениях частную производную на обыкновенную. Методика получения выражений для производных уже применялась в задаче №7. Поэтому в задаче используем готовые таблицы коэффициентов аппроксимирующих выражений из учебного пособия [  ]. В левом столбце таблицы перечислены производные для каждой точки аппроксимирующего интервала, а в названиях следующих столбцов – имена ординат. Алгебраическая сумма ординат, умноженных на соответствующий коэффициент таблицы, представит правую часть одного из уравнений общей системы.

Скачать файл