Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 17

Третий оператор позволяет обеспечить выдачу приближенного результата с заданным числом значащих разрядов, хотя уставка, выполненная в пункте меню Declare, может быть другая, например:

      € Rd(5)    ‚

APPROX¦———————, 4¦

         15     ƒ

[0.8666, 0.6666, 0.3333, 0.7333, 0.4666]

Четвертый оператор выполняет разложение выражения на простейшие сомножители относительно заданных аргументов, представляемых и в комплексной форме в возвращаемом результате.

        3      2                         

FACTOR(x  + 7·x  + 15·x + 25, Complex, x)

(x + 5)·(x + 1 + 2·î)·(x + 1 - 2·î)

Для выражения, генерирующего случайный вектор с целыми числами:

      € Rd(8)           ‚

FACTOR¦———————, Rational¦

         15            ƒ

„                                           2 †

¦  13    2    1     11     7        2·7    2  ¦

¦—————, ———, ———, —————, —————, 1, —————, ————¦

… 3·5    3    3    3·5    3·5       3·5     5 ‡

Представленные операторы можно вызывать по имени с фактическими параметрами, передаваемыми в факторизуемое выражение:

                   € Rd(a)           ‚

FRd(a, b) := FACTOR¦———————, Rational¦

                      b             ƒ

FRd(9, 15)

„                                           2      3 †

¦  13    2    1     11     7        2·7    2      2  ¦

¦—————, ———, ———, —————, —————, 1, —————, ————, —————¦

… 3·5    3    3    3·5    3·5       3·5     5    3·5 ‡

В пакетах DERIVE под Windows версий 4.0 и выше встроены операторы расчленения выражений (декомпозиция). К наиболее важным из них можно отнести операторы выделения правой RHS(u) или левой LHS(u) функции, из выражения, в котором функции связаны знаком отношения.

Если  u:=f(x)Äg(y), то первый оператор возвратит значение g(y), а второй – f(x). Здесь символ отношения .

           €„  x + 4·y + 5·z = 6  †           ‚

           ¦¦                     ¦           ¦

RS := SOLVE¦¦  2·x + y + 2·z = 3  ¦, [x, y, z]¦

           ¦¦                     ¦           ¦

           … 3·x + 7·y + 8·z = 9 ‡           ƒ

[ x = 0  y = -1  z = 2 ]

LHS(RS)` - RHS(RS)`

„   x   †

¦ y + 1 ¦

… z - 2 ‡

Декомпозиция выражений, представленных алгебраической суммой, осуществляется встроенным оператором TERMS(), который возвращает вектор с числом компонент, равных числу слагаемых со своими знаками:

       3      2             

TERMS(x  - 7·x  + 15·x - 25)

„ 3     2          †

…x , -7·x , 15·x, -25‡

Остальные операторы декомпозиций приведены в файле помощи Halp в разделе, который вызывается по имени упомянутых операторов.

Выполнение расчетных заданий

Методику применения математического пакета DERIVE рассмотрим на примерах семестрового расчетного задания. В задачах задания будем приводить пояснения по применению операторов пакета для реализации известных соотношений и определений из разделов курса высшей математики, изучаемых в институте. Грамотное применение пакета базируется на знаниях основ программирования на алгоритмических языках и понимании вычислительных методов решения задач.

Задача 1:Оценка инструментальной погрешности.

Исходные данные вводятся в ЭВМ как абсолютно точные числа и представляются в ней в виде чисел с плавающей точкой с относительной погрешностью в одну миллионную. Введенные данные  и  служат основой формирования двух векторов  и  по рекуррентным формулам:

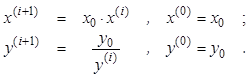
Вычислить скалярное произведение   по алгоритму:

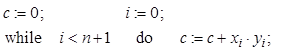
и оценить аналитически и численно инструментальную абсолютную и относительную погрешности.

Предварительные замечания.

Числа с плавающей точкой в общем виде представляются так:

 

где          характеристика (мантисса) числа, определяющая его точность;

 порядок числа;

 основание системы счисления (в наших примерах ).

Относительная погрешностью в одну миллионную (d=10^-6) говорит о том, что значащая часть  исходных чисел и промежуточных значений представляется шестью десятичными цифрами, а ограничение разрядности происходит с применением «правильного» округления.