Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 43

¦                                 1ƒ ¦

¦ h23:=RHS€(SOLVE(H   -A   ,[h23])) ‚ ¦

¦         ¦        2,3  2,3         ¦ ¦

¦                                 1ƒ ¦

¦ h33:=RHS€(SOLVE(H   -A   ,[h33])) ‚ ¦

¦         ¦        3,3  3,3         ¦ ¦

…                                 1ƒ ‡

Исполнив этот блок операторов, получим следующие значения для символьных переменных матрицы HU:

NotationDigits:=6

„  1.68552  †

¦ 0.160309  ¦

¦ -0.162340 ¦

¦  1.07226  ¦

¦ -0.346894 ¦

…  1.35530  ‡

Зная разложение матрицы А на произведение треугольных, решение исходного уравнения  можно теперь представить в виде системы из двух систем уравнений с треугольными матрицами:

Исполняем определение матрицы HL с высвеченной правой частью:

    „  1.68552       0         0    †

HL:=¦ 0.160309    1.07226      0    ¦

    … -0.162340  -0.346894  1.35530 ‡

Решение треугольной системы  производится тривиально: начиная с верхней, находим y1 , затем y2 и из последней строки – y3.

      €     €„  1.68552      0         0   †                                        ‚‚

Y:=RHS¦SOLVE¦¦ 0.160309   1.07226      0   ¦•[ y1  y2  y3 ]`+[ 3  2  1 ]`,[y1,y2,y3]¦¦

           … -0.16234  -0.346894  1.3553 ‡                                        ƒƒ

Y:=[ -1.77986  -1.59911  -1.36033 ]

Теперь, для присвоения числовых значений элементам, исполняем определение матрицы DHU и с найденным вектором Y решаем вторую систему с треугольной матрицей :

     „ -1.68552  -0.160309   0.16234 †

DHU:=¦     0     -1.07226   0.346894 ¦

     …     0         0       -1.3553 ‡

      €     €„ -1.68552  -0.160309   0.16234 †                              ‚‚

X:=RHS¦SOLVE¦¦     0     -1.07226   0.346894 ¦•[ x1  x2  x3 ]`-Y`,[x1,x2,x3]¦¦

           …     0         0       -1.3553 ‡                              ƒƒ

X:=[ 0.979921  1.81607  1.00371 ]

Для проверки правильности разложения перемножим найденные треугольные матрицы. Результатом должна оказаться матрица À.

HL•DHU

„ -2.84101   -0.270206  0.273629 †

¦ -0.270207  -1.17544   0.397985 ¦

…  0.27363   0.397986   -1.98352 ‡

Задача № 26: Система дифференциальных уравнений

Найти аналитическое решение и построить графики переходных процессов для системы линейных дифференциальных уравнений:

Здесь                    – вектор внешних воздействий на объект.

 – вектор решений.

Нужные числовые значения берутся из предыдущих пунктов задания:

   „ -2.84101   -0.270207   0.27363 †

A:=¦ -0.270207  -1.17545   0.397987 ¦,     b:=[3,2,1]

   …  0.27363   0.397987   -1.98353 ‡     ,

   „ „ 0.00708661  -0.0784251  -0.0297637 † †

   ¦ ¦ -0.0784251   0.867905    0.329385  ¦ ¦

   ¦ … -0.0297637   0.329385    0.125007  ‡ ¦

   ¦                                        ¦

   ¦   „ 0.144815   -0.113352  0.333158  †  ¦

P:=¦   ¦ -0.113352  0.0887259  -0.260777 ¦  ¦ – проекторы,

   ¦   … 0.333158   -0.260777  0.766459  ‡  ¦

   ¦                                        ¦

   ¦  „ 0.848098    0.191779    -0.303394 † ¦

   ¦  ¦ 0.191779    0.0433669  -0.0686063 ¦ ¦

   …  … -0.303394  -0.0686063   0.108535  ‡ ‡

¡:=[-1,-2,-3] – собственные значения матрицы A.

x0:=[1,2,3] – вектор начальных значений;

x:=[x1,x2,x3] – вектор искомых функций.

Общее решение неоднородного линейного дифференциального уравнения первого порядка, записанного в векторной форме, имеет следующее аналитическое представление:

,

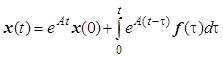где          – экспоненциальная функция матричного аргумента;

 – вектор-функция неоднородной части уравнения.

Построение операторов для общей формулы решения

Чтобы вычислить функцию с матричным аргументом , представим ее сначала в форме спектрального разложения, использованного в задаче 24:

В нотации пакета DERIVE это будет выглядеть следующим образом:

         ¡ ·t     ¡ ·t     ¡ ·t

          1        2        3  

eAt:=P ·ê    +P ·ê    +P ·ê    

      1        2        3      

Первое слагаемое общего решения вычислим так:

NotationDigits:=6

(eAt•[x0]`)`

„„            -t           -2·t           -3·t ††

¦¦ -0.239054·ê  +0.917585·ê    +0.321474·ê     ¦¦

¦¦          -t           -2·t            -3·t  ¦¦

¦¦ 2.64553·ê  -0.718231·ê    +0.0726939·ê      ¦¦