Информатика и выч. техника \ Программирование

Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 21

S(m,j):= ¤ (-1) ·COMB(m,k)·G

k=0 3,k+1+j

Здесь m задает порядок конечной разности для j-й точки таблично заданной функции, то есть, меняя j, мы для вычисления разностей будем использовать ординаты более далекие от начала таблицы. Если вычисление разностей выполнять для всех комбинаций m и j , то обращение к некоторым столбцам матрицы G приведет к выходу значений индексов за их дозволенные пределы изменения, на что пакет, при выполнении S(m,j), отреагирует выводом вопросительного знака (?). В этих местах в таблицу разностей оператором IF() вставим пустой символ в двойных кавычках.

Rzn:=VECTOR(VECTOR(IF(S(m,j)=?,"",S(m,j)),m,1,5),j,0,5)

Tkr:= APPEND([zg],APPEND(G,Rzn`)`)

 2 3 4 5 

¦ k x f ¦

¦ 0 0.7 -0.06 0.724 -1.136 0.924 -1.14 2.32 ¦

¦ 1 1.3 0.664 -0.412 -0.212 -0.216 1.18 "" ¦

Tkr:=¦ 2 1.9 0.252 -0.624 -0.428 0.964 "" "" ¦

¦ 3 2.5 -0.372 -1.052 0.536 "" "" "" ¦

¦ 4 3.1 -1.424 -0.516 "" "" "" "" ¦

5 3.7 -1.94 "" "" "" "" "" 

Еще одно полезное замечание по ускорению работы операторов программы. Если определение процедуры (оператора) подсвечено курсором вместе с ее (его) заголовком, то DERIVE производит вычисление согласно определению, не присваивая результат имени процедуры. Если курсором высветить лишь правую часть определения, то последнее заменяется результатом выполнения.

В последнем примере была сделана именно такая подсветка, поэтому имени Tkr теперь присвоено значение в виде полной таблицы на 7 строк и 8 столбцов. Польза от такого присвоения состоит в том, что единственный оператор с его новым значением можно передать из командной строки через буфер в другой файл этого же или другого сеансов пакета.

Задача 3: Построение многочленов по разностям

Таблично заданную функцию G(k) с целочисленным аргументом представить в виде разложения по факториальным многочленам и преобразовать его в степенные многочлены G(z) и G(x).

Пояснения

Значение таблично заданной функции g(i+n), расположенной на n строк ниже i-й строки через оператор конечной разности D выражается так:

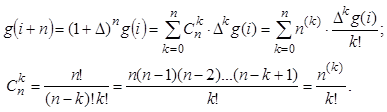
С первой строкой таблично заданной функции совмещено начало координат для целочисленного аргумента, где . В принципе таблица может иметь любой размер. Если в таблице строка, то такая таблица определяет степенные многочлены, у которых степени не выше , и, следовательно, их конечные разности порядков выше , равны нулю. Поэтому значение ординаты функции находящейся на строке можно представить через конечные разности нулевой строки следующим образом:

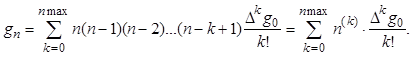
Если взять равным для заданной таблицы конечной разности максимального порядка, то получим интерполяционный многочлен целочисленного аргумента . Так как , то, выразив отсюда и подставив в , получим интерполяционный многочлен действительной переменной .