Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 26

                €d ‚-(j+1) €d ‚j+1          

g2x(n,k,m,j):= Md(n,k,m) - ¦——¦       ¦——¦    Md(n,k,m)

       ddƒ       ddƒ             

Вызов на исполнение этой процедуры с конкретными параметрами условия задачи даст следующий конечно-разностный оператор:

g2x(2, 3, 5, 5)

5         4                 d      11·d        3    2 - ———— + ——————— + 2·d  + d    12       12

Разделив результат на квадрат шага по действительной переменной и приписав справа разностным операторам различных порядков обозначение ординаты функции на нулевой строке табличной функции, получим первую форму представления второй производной через повторные конечные разности:

           5         4         3         2   

           g  - 11· g  - 24· g  - 12· g  

             0         0         0         0

g `` = - ————————————————————————————————————

3                             2             

                           12·h

Подстановка числовых значений разностей и вычисление дадут следующее значение второй производной для четвертой строки функции:

          2.32 - 11·(-1.14) - 24·0.924 - 12·(-1.136)            

g `` = - ———————————————————————————————————————————— = -1.46203

 3                                2                             

                            12·0.6                              

Проверка значения производной

Для проверки полученного значения второй производной дважды продифференцируем интерполяционный многочлен, построенный для этой же табличной функции в 3-й задаче, и подставим в выражение производной значение аргумента функции с четвертой строки.

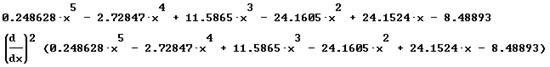
         3            2                    

4.97255·x  - 32.7416·x  + 69.519·x - 48.321

           3              2                      

4.97255·2.5  - 32.7416·2.5  + 69.519·2.5 - 48.321

-1.46241

Вторая форма разностного выражения производной

Чтобы выразить эту же производную через ординаты табличной функции , каждую i-тую повторную разность заменим соответствующей алгебраической суммой, вычисляемой по формуле:

          i      i - k               

y(i) :=  ¤  (-1)     ·COMB(i, k)·y .

         k=0                       k

Проверим в работе эту процедуру для нужных порядков разностей:

[VECTOR(y(i), i, 2, 5)]` =

„            y  - 2·y  + y              † ¦             2      1    0             ¦ ¦         y  - 3·y  + 3·y  - y          ¦ ¦          3      2      1    0         ¦ ¦     y  - 4·y  + 6·y  - 4·y  + y       ¦ ¦      4      3      2      1    0      ¦ ¦ y  - 5·y  + 10·y  - 10·y  + 5·y  - y  ¦  5      4       3       2      1    0 ‡

Теперь подстановим разностные выражения и выполним упрощение:

          y(5) - 11·y(4) - 24·y(3) - 12·y(2)

g `` = - ————————————————————————————————————————

 3                             2                 

                           12·h                  

Результатом является вторая форма представления производной:

          y  - 16·y  + 30·y  - 16·y  + y  

           5       4       3       2    1

g `` = - —————————————————————————————————

 3                         2              

                       12·h               

Подстановка числовых данных из таблицы функции и вычисление дает

          -1.94 - 16·(-1.424) + 30·(-0.372) - 16·0.252 + 0.664            

g `` = - —————————————————————————————————————————————————————— = -1.46203

 3                                     2                                  

                                 12·0.6                                   

Вычисления производной и по второй форме показали тот же результат. Расхождение в младших разрядах связаны с ограничением разрядности кодов в интерполяционном многочлене.

Задача №8: Аппроксимирующие многочлены

Методом наименьших квадратов для таблично заданной g(x) получить аппроксимирующие степенные полиномы нулевой, первой, второй и третьей степеней   и  изобразить их на одном графике.

Основа метода наименьших квадратов