Информатика и выч. техника \ Программирование

Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 31

  € ¦Yr(1000)-Yapp(1000)¦ ‚

Zn¦——————————————————————-¦

         ¦Yr(1000)¦      ƒ

          -5

1.37939·10  

Задача № 14: Полиномы Чебышева

Степенными полиномами Чебышева  относительно переменной x  () являются решения линейного разностного уравнения второго порядка:

,

c начальными условиями      и   .

Найти  аналитическое  выражение  и  вычислить  значение  полинома Чебышева i-той степени, если  и i = 4. Проверить  вычисления непосредственно по заданной рекуррентной формуле. Найти положение нулей и экстремумов у многочленов Чебышева в общем виде и для заданных выше x и i. Оценить модуль максимально возможного значения полинома в точках экстремумов. В качестве  берутся || из таблицы исходных данных.

Решение разностного уравнения

В задаче №13 уже проводилось решение однородного разностного уравнения пункт за пунктом. Однако DERIVE в утилите RECUREQN.MTH имеет набор процедур, которые решают разностные уравнения первого и второго порядков. Воспользуемся одной из них:

"LIN2_CCF_BV(p, q, r, x, x0, y0, x2, y2)",

где         p, q, r, x – соответственно коэффициенты при слагаемых,

функция в правой части уравнения и независимая переменная;

x0, y0, x2, y2 – координаты двух известных точек рекуррентной последовательности.

Для заданного уравнения параметры списка будут следующими:

T(i):=LIN2_CCF_BV(-2·x,1,0,i,0,1,1,x)

Определим область определения переменной x в пункте меню

Declare  Variable Domain: Variable x:  Declare: Open interval: (-1, 1)

x:­Real (-1, 1)

Исполнение процедуры LIN2_CCF_BV() дает следующую формулу:

         €           ¹·i ‚

T(i):=COS¦i·ASIN(x)-————-¦:= COS(i·ACOS(x))

                     2  ƒ

NotationDigits:=6

              4     2    

T(4)     8·x - 8·x  + 1

       lim        T(4)          0.983702

x˜-0.06/(2·0.664)     

Модуль максимальных значений любых многочленов Чебышева равен 1.

Нули многочленов Чебышева

Нули многочлена Чебышева найдем, приравнивая общее выражение многочлена и решая полученное уравнение относительно x :

COS(i·ACOS(x))=0

[SOLVE(COS(i·ACOS(x)),x)]`

i:­Integer (0, –)

„     €  ¹   ¹·(i-1)   ¹     €  ¹  ‚‚ †

¦ x=IF¦-——-<————————-“——-,COS¦————-¦¦ ¦

…       2     2·i     2      2·i ƒƒ ‡

Здесь получено лишь по одному (максимальному по модулю) корню для каждого i-того многочлена Чебышева. Для i=4 все корни будут равны:

[SOLVE(COS(4·ACOS(x)),x)]`

„ x=0.923879  †

¦ x=-0.923879 ¦

¦ x=0.382683  ¦

… x=-0.382683 ‡

Положение экстремумов многочленов Чебышева

Продифференцируем общее выражение многочлена Чебышева по x и результат приравняем нулю. Полученное уравнение решим относительно .

     €d                  ‚

SOLVE¦—— COS(i·ACOS(x)),x¦

     dx                 ƒ

i:­Integer (0, –)

„    €  ¹   ¹·(i-2)   ¹     € ¹ ‚‚†

¦x=IF¦-——-<————————-“——-,COS¦——-¦¦¦

…      2     2·i     2      i ƒƒ‡

Для многочлена Чебышева 4-й степени экстремумы будут в точках:

     €d                  ‚

SOLVE¦—— COS(4·ACOS(x)),x¦

     dx                 ƒ

„       ‹2      ‹2 †

¦x=0,x=———-,x=-———-¦

…        2       2 ‡

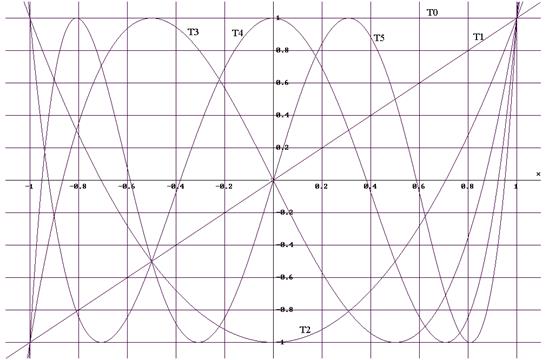
Графики первых шести многочленов Чебышева показаны ниже:

Вычисление по рекуррентному алгоритму

Ti(i):=(ITERATE(„Y ,2·x·Y -Y †,Y,[1,x],i))

                … 2      2  1‡             

                                          1

                  4      2   

Ti(4)       8·x  - 8·x  + 1

Результат совпадает с вычислением по общей формуле.

Задача № 15: Разложение по многочленам Чебышева 

Составить таблицу выражений многочленов Чебышева через их степенные представления и, наоборот: представить степени  через многочлены Чебышева  для  i = 0, 1, ... , 5.  Благодаря этим соответствиям получить разложение по многочленам Чебышева степенного представления интерполяционного многочлена G(x), полученного в задаче № 3.

Получение степенных представлений

Для построения таблицы степенных представлений многочленов Чебышева можно воспользоваться рекуррентным алгоритмом, рассмотренным в задаче №14, либо такое разложение получить с помощью команды Expand в DERIVE:

    T(x,i):=EXPAND(COS(i·ACOS(x)),Trivial,x)

„VECTOR(t   =T(x,i),i,0,5)†`

Скачать файл