Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 30

Проведенные вычисления показывают, что квадратурные формулы достаточно успешно могут применяться и для иррациональных функций. Точность вычислений может оказаться даже существенно выше, чем вычисление интеграла по усеченному степенному ряду, приближенно представляющему подинтегральную функцию.

Задача № 13: Уравнение рекуррентного процесса

Найти аналитическое выражение для Y(n,x), описываемого рекуррентным вычислительным процессом в соответствии со следующим алгоритмом :

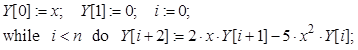
Оценить величину результата и погрешность прямого вычисления Y(n,x) по алгоритму и то же самое – по аналитически найденному решению для n = 1000 и x = 1, если относительная погрешность операций с плавающей точкой равна  и вычисление производится с 6 десятичными знаками.

Аналитическое решение разностного уравнения

Представим рекуррентную формулу заданного алгоритма однородным разностным уравнением второго порядка в неявном виде:

Найдем корни характеристического уравнения:

       2             2   

SOLVE(s - 2·x·s + 5·x , s)

[s = x + 2·î·x, s = x - 2·î·x]

Общее решение однородного разностного уравнения будет:

              i             i

y=c1·(x+2·î·x) +c2·(x-2·î·x)

Коэффициенты c1 и c2 найдем из системы уравнений, которую получим после подстановки значений y для i=0 и i=1

SOLVE([c1+c2=x,x·(c1+c2)+î·x·(2·c1-2·c2)=0],[c1,c2])

„     x   î·x       x   î·x  †

¦ c1=——-+————-  c2=——--————- ¦

…     2    4        2    4   ‡

Подставив найденные коэффициенты и заданное значение x=1, получим:

          €€ x   î·x ‚          i € x   î·x ‚          i‚

y(i):=lim ¦¦——-+————-¦·(x+2·î·x) +¦——--————-¦·(x-2·î·x) ¦

      x˜1  2    4  ƒ             2    4  ƒ           ƒ

           €                           €      € 1 ‚  ¹·i ‚ ‚

           ¦                        SIN¦i·ATAN¦——-¦-————-¦ ¦

       i/2 ¦   €      € 1 ‚  ¹·i ‚            2 ƒ   2  ƒ ¦

y(i):=5   ·¦COS¦i·ATAN¦——-¦-————-¦+———————————————————————-¦

                     2 ƒ   2  ƒ             2           ƒ

                                        348

y(1000) = -6.817561441118838117616839·10   

Точное вычисление по рекуррентной формуле

Для вычисления по рекуррентной формуле заданного алгоритма используем оператор итерационных подстановок:

        €„             2   †          ‚

ITERATES¦¦Y ,2·x·Y -3·x ·Y ¦,Y,[x,0],3¦

        … 2      2       1‡          ƒ

„   x      0   †

¦            3 ¦

¦   0    -3·x  ¦

¦     3      4 ¦

¦ -3·x   -6·x  ¦

¦     4      5 ¦

… -6·x   -3·x  ‡

Убедившись в правильности рекуррентных подстановок, перепишем теперь этот оператор так, чтобы выводилась лишь первая компонента последнего вектра:

           €       €„             2   †          ‚‚

Yr(i):=lim ¦ITERATE¦¦Y ,2·x·Y -5·x ·Y ¦,Y,[x,0],i¦¦

       x˜1        … 2      2       1‡          ƒƒ

                                                   1

Yr(1000)

                              348

-6.817561441118838117616839·10   

Точные вычисления по аналитической формуле и по итерационному алгоритму полностью совпадают.

Рекуррентные вычисления с ограниченной точностью

Для вычислений с плавающей точкой используем утилиту, представленную набором 7 операторов в первой задаче. Для этого сохраним эти 7 операторов, например, в файле с именем ZNFLOOR.MTH и загрузим его в рабочую сессию DERIVE как утилиту. После этого для выполнения каждого арифметического действия будем использовать оператор Zn(...).

Так, вычислительное ядро рекуррентной формулы будет таким:

         €               €    2    ‚‚

Jadro:=Zn¦2·Zn(x·Y )-5·Zn¦Zn(x )·Y ¦¦

                 2              1ƒƒ

Yapp(i):=lim (ITERATE(„Zn(Y ),Jadro†,Y,[x,0],i))

         x˜1          …    2       ‡             

                                                1

Yapp(1000)

                              348

-6.817655481777573997681131·10   

Относительная погрешность вычисления по рекуррентной формуле в системе с плавающей точкой с 6 значащими разрядами вычисляется так:

¦Yr(1000)-Yapp(1000)¦

——————————————————————-

       ¦Yr(1000)¦      

                             -5

1.379388503471219761021789·10  

или с округлением результата: