Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 7

Табулирование функций

Таблицей в DERIVE является вектор, тип компонент которого определяется значениями табулируемой функции. Это встроенный оператор, общий вид записи которого представляется строкой следующего вида:

VECTOR(y,x,x0,xk,h)

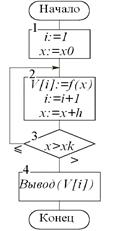Здесь первый элемент списка y является функцией аргумента x, который будет принимать значения от  x0  до  x≤xk  путем циклического добавления к текущему значению значения шага h. Формальный параметр y может быть представлен выражением  любого типа, лишь бы в него входил аргумент x, значения которого будут изменяться. Этим оператором простая скалярная функция превращается в решетчатую функцию, представленную вектором, размерность которого является максимальным целым числом k, не превышающем значения . Например, по записи в командной строке

VECTOR(ê^(-x), x, 1, 3, 0.7)

после выполнения будет выведен вектор следующего вида:

[0.367879, 0.182683, 0.0907179]

Построение таблиц-векторов с компонентами в форме матриц продемонстрируем на матрице следующего вида:

Mx(x, y) := [[x^2, y·SIN(x)], [y, EXP(-x)]]

            „  2           †

            ¦ x   y·SIN(x) ¦

Mx(x, y) := ¦              ¦

            …  y   EXP(-x) ‡

VECTOR(Mx(x, y), x, 1, 3, 1)

„„ 1  0.01745·y †  „ 4  0.03489·y †  „ 9  0.05233·y ††

¦¦              ¦, ¦              ¦, ¦              ¦¦

…… y   0.3678   ‡  … y   0.1353   ‡  … y   0.04978  ‡‡

Такие циклические операции могут производиться по нескольким переменным путем вложения операторов VECTOR() друг в друга, например, для матрицы Mx(x, y) после табуляции по переменной x , можно выполнить табуляцию (оцифровку) по переменной y :

VECTOR(VECTOR(Mx(x, y), x, 1, 3, 1), y, 0.2, 0.5, 0.2)

Результатом выполнения вложенных циклических операторов будет прямоугольная матрица (2´3) с матричными элементами (2´2):

„ „  1   0.00349 †  „  4   0.006979 †  „  9   0.01046 † †

¦ ¦              ¦  ¦               ¦  ¦              ¦ ¦

¦ … 0.2  0.3678  ‡  … 0.2   0.1353  ‡  … 0.2  0.04978 ‡ ¦

¦                                                       ¦

¦ „  1   0.00698 †  „  4   0.01395 †   „  9   0.02093 † ¦

¦ ¦              ¦  ¦              ¦   ¦              ¦ ¦

… … 0.4  0.3678  ‡  … 0.4  0.1353  ‡   … 0.4  0.04978 ‡ ‡

Операторному выражению с вложенными циклами можно дать имя с формальным параметром x, определив тем самым функцию, возвращающую в качестве результата матрицу с фактическим параметром. Над такой функцией можно выполнять любые алгебраические, интегральные и дифференциальные операции, которые затронут все компоненты матрицы одновременно, например: выражение

                        i/j                    

MM(x) := VECTOR(VECTOR(x   , i, 1, 3), j, 1, 2)

определяет двумерный массив (2´3) следующего вида:

„      2    3  †

¦  x  x    x   ¦

¦              ¦

¦          3/2 ¦

… ‹x   x  x    ‡

Если необходимо сформировать вектор v с двумя компонентами, из которых первая является определенным интегралом от MM(x) , а вторая – первой производной от MM(x) , то в командной строке и в алгебраическом окне должны быть следующие записи:

v := [INT(MM(x), x, 0, b), DIF(MM(x), x)]

     „ b                   †

     ¦ˆ            d       ¦

v := ¦‰  MM(x) dx, —— MM(x)¦

     … 0           dx      ‡

После выполнения последнего оператора будет получен вектор

„„     2       3       4    †                         †

¦¦    b       b       b     ¦  „                  2  †¦

¦¦   ————    ————    ————   ¦  ¦    1    2·x   3·x   ¦¦

¦¦     2       3       4    ¦  ¦                     ¦¦

¦¦                          ¦, ¦    1          3·‹x  ¦¦

¦¦     3/2     2       5/2  ¦  ¦ ——————   1   —————— ¦¦

¦¦  2·b       b     2·b     ¦  …  2·‹x           2   ‡¦

¦¦ ————————  ————  ———————— ¦                         ¦

……     3       2       5    ‡                         ‡

Итеративный цикл

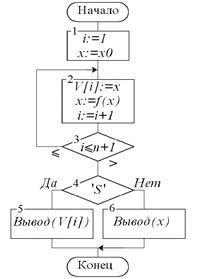Итеративный (или повторный) процесс подстановки значений функции вместо значений своих аргументов. Встроенными являются два оператора, отличающиеся присутствием или отсутствием одной буквы S  в конце имени оператора, это

ITERATES(f(x),x,x0,n)

ITERATE(f(x),x,x0,n)