Операторы присваивания можно представить программным блоком, который выполняется от начала до конца. Внешне запись блока представляется вектором, компонентами списка которого являются операторы присваивания. Присваивание значений переменным, стоящим в левой части операторов, происходит в порядке их перечисления в списке вектора-блока, которому, естественно, может быть дано и имя, например:
L_blok:=[x:=7, y:=x^2, z1:=f(x, y)]
В результате вызова блока L_blok на исполнение сначала х, затем у получат значения 7 и 49 соответственно, после чего в определенную ранее функцию f(x, y) вместо х и у будут подставлены их новые фактические значения и результат вычисления будет присвоен переменной z1. Присвоенные таким образом значения будут сохраняться до тех пор, пока другими операторами присваивания их значения не будут изменены. Таким способом удобно инициировать начальные значения переменным, которые в результате работы с пакетом могут принимать другие значения.
Все имена операндов, которым что-то присваивалось, независимо от места их расположения на поле операторов, передают свои значения в любые формульные и операторные выражения, где встречается их имя.
Важным при исполнении операторов присваивания является то, какие части на исполнение помечаются курсором. Если курсор выделяет оператор целиком или только его левую часть (имя), то выводится результат вычислений. Если же выделяется лишь правая часть, то в операторе присвоения происходит замена его правой части результатом вычислений. Этот способ удобен для ускорения вычислений в случаях, когда в операторах и формулах содержится глубокое иерархическое вложение множества функций, вызываемых по именам.
Среди встроенных операторов-функций для построения программ находят применение операторы стандартных функций для обычных и комплексных аргументов, функции с векторными аргументами, циклические и условные операторы, операторы решения уравнений и и их систем и многие другие...
Набор встроенных операторов позволяет составлять программы стандартных процедур, которые в DERIVE называют утилитами. Подборка процедур на заданную тему, будучи загруженной в выполняемую задачу как утилита, на экране монитора не отображается, однако все имена функций со списками параметров становятся доступными наравне со встроенными функиями.
В DERIVE имеются по крайней мере 4 оператора, которые реализуют циклические вычисления, а именно: вычисление суммы членов ряда, вычисление произведения членов ряда, табулирование функции и подстановка значения функции в качестве ее же аргумента.
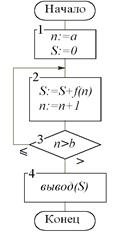Ряд может быть задан
аналитическим выражением n-го члена ряда.
Переменной цикла при накоплении частичных сумм служит целого типа переменная n, для которой необходимо задать нижний и верхний
пределы изменения. Задание выражения n-го
члена ряда и пределов суммирования осуществляется в строчной форме в командной
строке. Если на экране монитора нужное выражение n-го
члена ряда уже сформировано, то можно воспользоваться «горячей» клавишей с
изображением знака Σ . Например, для вычисления суммы ряда 
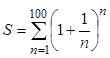в командной строке необходимо набрать
следующий текст:
¤((1 + 1/n)^n, n, 1, 100)
На поле алгебраического окна после щелчка мыши по кнопке ОК эта запись будет представлена в знакомой математической форме:
100 1 n
¤ ¦1 + ¦
n=1 n
Выделив курсором на поле алгебраического окна это выражение и нажав «горячую» клавишу со значком ≈ получим результат суммирования в форме, определенной ранее, например, такими установками
Declare
Input
Settings Output Options:
Notation: Decimal 
Digits: 12
в виде десятичного дробного числа с 12 знаками:
266.035948407
Если для получения результата использовать «горячую» клавишу ═ , то при установках, соответствующих символьным преобразованиям:
…Mode: ExactBranch: Principal
на экран монитора будет выведено число, в виде рациональной дроби, числитель и знаменатель которой представлены абсолютно точными целыми числами. Количество их разрядов может оказаться необозримым.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.