Информатика и выч. техника \ Программирование

Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 23

¦         0.25·m·(m+1)·(m-1)·(m-2)         ¦

¦       0.2·m·(m+1)·(m-1)·(m-2)·(m-3)      ¦

… 0.166666·m·(m+1)·(m-1)·(m-2)·(m-3)·(m-4) ‡

Умножение этих сумм на конечные разности, начиная с разности нулевого порядка, осуществим следующим оператором:

        „      €          fm(m+1,k+1)       ‚†

VSL(m):=¦VECTOR¦Tkr     ·————————————-,k,0,5¦¦`

        …         2,3+k     (k+1)!         ƒ‡

„                 -0.06·(m+1)                †

¦                0.362·m·(m+1)               ¦

¦           0.189333·m·(m+1)·(1-m)           ¦

¦         0.0385·m·(m+1)·(m-1)·(m-2)         ¦

¦      0.0095·m·(m+1)·(1-m)·(m-2)·(m-3)      ¦

… 0.00322222·m·(m+1)·(m-1)·(m-2)·(m-3)·(m-4) ‡

Теперь остается лишь просуммировать все составляющие вектора VSL(m), чтобы получить окончательное выражение суммы функционального ряда в виде функции от верхнего предела m .

            € 6                       ‚

S(m):=EXPAND¦ ¤  (VSL(m))   ,Trivial,m¦.

            j=1         j,1          ƒ

                 6         5           4           3

S(m)=0.00322222·m -0.0385·m +0.166555·m -0.362166·m +

           2                

+0.192222·m +0.702666·m-0.06.

Для m=5 мы должны получить сумму всех ординат табличной функции:

S(5)= -2.88.

Проверка полученной формулы суммирования

Проверку выполним непосредственным суммированием всех ординат заданной табличной функции, расположенных в третьем столбце Tkr:

 7        

 ¤  Tkr          -2.88

i=2    i,3

Проверка показала полное совпадение вычисленных значений.

Задача №5: Повторные разделенные разности

Составить таблицу упорядоченных разделенных разностей для g(x). Проверить правильность таблицы для разделенной разности  по формуле ее аналитического представления.

Основные определения и формулы

О разделенных разностях говорят тогда, когда функциональная зависимость представляется табличной функцией с неравными интервалами и неранжированными значениями аргумента. Для таблицы функции с (n+1) строкой разделенную разность определяют и обозначают следующим образом:

,  

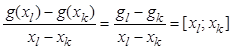Общее число разделенных разностей в таблице из (n+1) строк равно числу сочетаний из (n+1) по 2. Для построения многочлена, проходящего через (n+1) табличную точку, достаточно использовать n разностей. Поэтому разумно вычислять разделенные разности только по рядом стоящим в таблице значениям функции. В этом случае говорят об упорядоченных разделенных разностях, которые обозначают для i-той строки таблицы (i=0, 1, 2, …,n) следующим образом: .

Повторная разность от разделенной разности есть разделенная разность второго порядка:

В общем случае разделенная разность j-го порядка имеет вид:

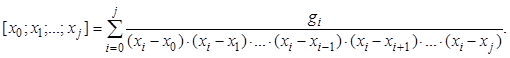
Построение упорядоченных разделенных разностей

В качестве исходных данных используем табличную функцию:

   „  0.7    1.3    1.9     2.5     3.1    3.7  †

g:=¦                                            ¦

   … -0.06  0.664  0.252  -0.372  -1.424  -1.94 ‡

Для вычисления i-того слагаемого в выражении повторной разности порядка j (j = 0,1,…,5) для заданной функции g необходимо в числителе дроби поместить значение i-той ординаты функции (i = 0,1,…,5). Кроме того, порядок и количество разностей зависит от того, какую строку таблично заданной функции мы будем принимать за начальную, поэтому для выбираемой ординаты функции введем смещение n (n = 0,1,…,5) вниз по таблице. Учитывая сказанное, оператор вычисления разделенной разности Rzn(j,n) можно представить в следующем виде:

                          g`                     

           j                [1+i+n,2]            

Rzn(j,n):= ¤  ——————————————————————————————————-

          i=0   j                                

                £  IF(i=k,1,g`       -g`       )

               k=0            [1+i,1]   [1+k,1]  

В знаменателе вычисляются произведения разностей аргументов, которые определяют порядок вычисляемой разделенной разности. Условный оператор в этом произведении вместо нулевой скобки, где i=k, подставляет единицу.

В сформированном операторе будут такие сочетания (j,n), когда j>n . Для этих случаев пакет будет выдавать неопределенной значение в виде вопросительного знака (?). Чтобы заменить его на "" используем условный оператор:

Скачать файл