Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 44

¦¦           -t          -2·t           -3·t   ¦¦

……  1.00402·ê  +2.11098·ê    -0.115001·ê       ‡‡

Экспоненциальную функцию с матричным аргументом, входящую под знак интеграла, используя формулу спектрального разложения, представим и вычислим аналогичным образом:

          ¡ ·(t-¼)     ¡ ·(t-¼)     ¡ ·(t-¼)

           1            2            3      

eAt¼:=P ·ê        +P ·ê        +P ·ê        

       1            2            3          

Интегральный член общего решения запишим и вычислим так:

 t              

ˆ               

‰  eAt¼•[b]` d¼`

 0              

„„           -t           -2·t           -3·t          ††

¦¦ 0.165354·ê  -0.270449·ê    -0.874819·ê    +0.979914 ¦¦

¦¦           -t           -2·t           -3·t          ¦¦

¦¦ -1.82991·ê  +0.211690·ê    -0.197821·ê    +1.81605  ¦¦

¦¦            -t           -2·t           -3·t         ¦¦

…… -0.694485·ê  -0.622189·ê    +0.312953·ê    +1.00372 ‡‡

Общее выражение для решения получим в виде суммы:

€           t             ‚

¦          ˆ              ¦

¦eAt•[x0]`+‰  eAt¼•[b]` d¼¦`

           0             ƒ

„„             -t           -2·t           -3·t          ††

¦¦ -0.0737006·ê  +0.647135·ê    -0.553345·ê    +0.979914 ¦¦

¦¦            -t           -2·t           -3·t           ¦¦

¦¦  0.815620·ê  -0.506540·ê    -0.125127·ê    +1.81605   ¦¦

¦¦             -t          -2·t           -3·t           ¦¦

……   0.309541·ê  +1.48879·ê    +0.197951·ê    +1.00372   ‡‡

Установившееся значение переходного процесса вычислим так

    €           t             ‚

    ¦          ˆ              ¦

lim ¦eAt•[x0]`+‰  eAt¼•[b]` d¼¦`

t˜–            0             ƒ

„„ 0.979914 ††

¦¦  1.81605 ¦¦

……  1.00372 ‡‡

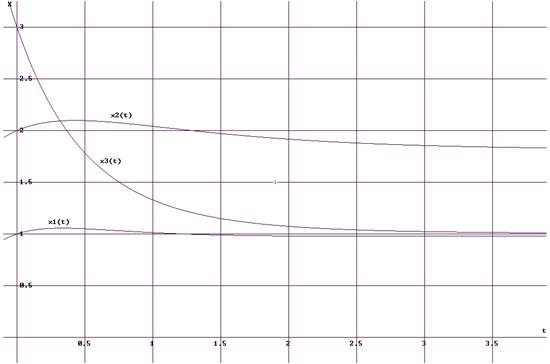
На рисунке показаны кривые векторного переходного процесса x(t).

Список использованной литературы

1.  Дьяконов В.П. Справочник по системе символьной математики DERIVE. – М.: «СК Пресс», 1998. – 256 с.

2.  Калашников В.И. Введение в численные методы: Учеб. пособие. – Харьков: НТУ “ХПИ”, 2002. – 132 с.

3.  Пакет символьной математики DERIVE for Windows версий 4.02, 5.0, 6.0 и выше

Варианты числовых значений к задачам

В таблице приведены варианты табличного задания функции , полученные для   .

Для вариантов с 1 по 100 в колонке «» значение  из таблицы берется со знаком плюс, а для вариантов от 101 до 200 – со знаком минус