Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 28

NotationDigits:=4

„                        -0.48                       †

¦                   1.226-0.7756·x                   ¦

¦                       2                            ¦

¦              -0.4345·x +1.136·x-0.4204             ¦

¦                  3        2                        ¦

¦          0.3305·x -2.616·x +5.335·x-2.618          ¦

¦         5        4        3        2               ¦

… 0.2486·x -2.728·x +11.58·x -24.16·x +24.15·x-8.488 ‡

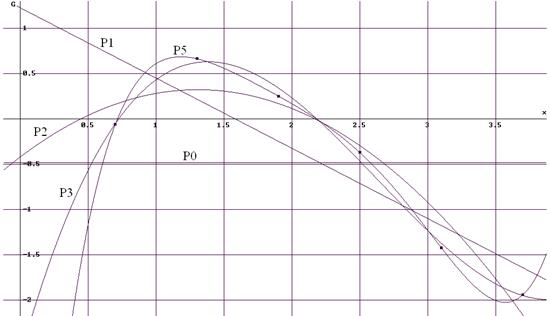
Кривые аппроксимирующих многочленов.

Как видим, многочлен 5-й степени строго проходит через заданные таблицей точки и равен многочлену G(x) из 3-й задачи.

Задача № 9: Конечные разности многочленов

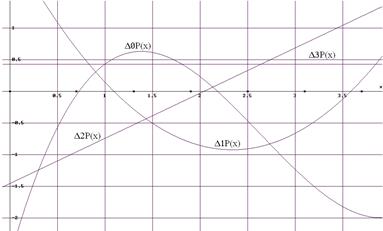
Для аппроксимирующего полинома третьей степени  получить аналитические выражения  , n=0,1,2,3,4  и все конечно-разностные  кривые изобразить на одном графике.

Решение задачи

Выразим повторные разности многочлена согласно определению:

                       3        2               

0P(x):=(P(x):=0.3305·x -2.616·x +5.335·x-2.618)

1P(x):=0P(x+h)-0P(x)

2P(x):=1P(x+h)-1P(x)

3P(x):=2P(x+h)-2P(x)

В вектор повторных разностей подставим шаг по табличной функции:

 lim  [ 0P(x) 1P(x) 2P(x) 3P(x) ]`

h˜0.6                                    

APPROX(EXPAND( lim  [ 0P(x) 1P(x) 2P(x) 3P(x) ]`,Trivial,x),6)

              h˜0.6                                                  

„         3        2               †

¦ 0.3305·x -2.616·x +5.335·x-2.618 ¦

¦              2                   ¦

¦      0.5949·x -2.782·x+2.330     ¦

¦          0.7138·x-1.455          ¦

…              0.4283              ‡

Задача № 10в: Квадратурные формулы

Вывести квадратурную формулу для вычисления определенных интегралов с пределами [-1,1] от подынтегральных функций f(t), принадлежащих классу степенных многочленов степеней {0, 1, 2, 3}.

Использовать значения функции в точках, обеспечивающих получение формул наивысшей алгебраической степени точности.

Теоретические предпосылки

Параметрами квадратурной формулы, которые необходимо найти, являются коэффициенты при значениях полиномиальной подынтегральной функции и значения ее аргументов, в которых она вычисляется.

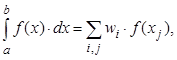
где          – параметры квадратурной формулы,

 – интегрируемая функция, не имеющая особенностей в [a,b].

Для данного задания [a,b]=[-1, 1]. Вид квадратурной формулы с четырьма параметрами (), определяющими заданный класс степенных подынтегральных функций , для которых квадратурная формула должна быть абсолютно точна, будет таким:

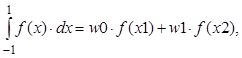
Неизвестные параметры этой формулы находятся из системы уравнений, получаемой путем подстановки вместо подинтегральной функции базисных функций заданного класса.

Решение задачи

Определим вектор базисных функций в командной строке:

s:=[x^0,x^1,x^2,x^3]

Определяем значения подинтегральной функции в параметрических точках (x1, ) внутри интервала интегрирования:

fx1(s):=LIM(s,x,x1)

fx2(s):=LIM(s,x,x2)

Уравнение для i-той базисной функции из вектора s будет:

q(i):=INT(s™i,x,-1,1)=w0·fx1(s™i)+w1·fx2(s™i)

Полную систему уравнений для нахождения параметров квадратурной формулы получим подстановкой всех базисных функций:

[VECTOR(q(i),i,1,4)]`

„      2=w0+w1      †

¦   0=w0·x1+w1·x2   ¦

¦  2       2      2 ¦

¦ ——-=w0·x1 +w1·x2  ¦

¦  3                ¦

¦         3      3  ¦

…  0=w0·x1 +w1·x2   ‡

Решение этой системы выполним так. Из первых двух уравнений найдем выражения для w0 и w1 через x1 и x2. Из двух последних найдем аналогичные выражения. Приравняв выражения одноименных параметров w0 и w1, получим уравнения для нахождения x1 и x2.

w01:=SOLVE(VECTOR(q(i),i,1,2),[w0,w1])

w23:=SOLVE(VECTOR(q(i),i,3,4),[w0,w1])

„      2·x2        2·x1  †

¦ w0=——————-  w1=——————- ¦

…     x2-x1       x1-x2  ‡

„          2·x2                2·x1      †

¦ w0=——————————————-  w1=——————————————- ¦

¦         2                   2          ¦

…     3·x1 ·(x2-x1)       3·x2 ·(x1-x2)  ‡

Теперь из полученных решений выделяем значения для w0 и ищем решение относительно x1:

SOLVE((RHS(w01))™1™1=(RHS(w23))™1™1,x1)

„    ‹3       ‹3            †

¦x1=———-,x1=-———-,x1=–,x1=-–¦

…     3        3            ‡