Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 29

SOLVE((RHS(w01))™1™2=(RHS(w23))™1™2,x2)

„    ‹3       ‹3            †

¦x2=———-,x2=-———-,x2=–,x2=-–¦

…     3        3            ‡

Результаты решения дают две пары различных значений параметров x1 и x2:   и , то есть  x1=-x2 . Подставив такие значения в выражения для w0 и w1 , получим w0=w1=1.

Таким образом, окончательный вид квадратурной формулы для данного условия, будет таким:

Задача № 11: Проверка квадратурной формулы

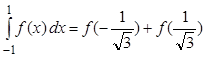
С помощью квадратурных формул, полученных в задаче № 10, вычислить определенный интеграл от степенного представления интерполяционного многочлена Лагранжа (Ньютона), полученного в задаче  № 6 в пределах от  до , и сравнить его с аналитически вычисленным значением определенного интеграла по первообразным многочлена.

Приведение заданного интеграла к квадратурной формуле

Степенной многочлен, полученный в задаче №6 и проходящий через четыре точки, имеет следующий вид:

g(x):=0.712962·x^3-4.35832·x^2+7.72027·x-3.57315

Для проверки точности квадратурной формулы сначала аналитически вычислим значение интеграла от g(x) в заданных пределах [x0, x3]=[0.7, 2.5]:

 2.5        

ˆ           

‰    g(x) dx    =   0.521149

 0.7        

Прежде, чем применять квадратурную формулу, заданные пределы [x0, x3] необходимо преобразовать к каноническим значениям [-1,1]. Для этого переменную x заменим переменной t, используя линейное соотношение  и . Коэффициенты a и b найдем непосредственной подстановкой соответствующих пределов для x и t .

SOLVE([x0=a+b·(-1),x3=a+b·1],[a,b])

„    x0+x3      x3-x0  †

¦ a=——————-  b=——————- ¦

…      2          2    ‡

„    x0+x3      x3-x0  † „    0.7+2.5      2.5-0.7  †

¦ a=——————-  b=——————- ¦=¦ a=————————-  b=————————- ¦

…      2          2    ‡ …       2            2     ‡

Подынтегральная функция для канонических пределов предстанет теперь в следующем формульном и числовом виде:

       € 0.7+2.5   2.5-0.7   ‚  2.5-0.7

G(t):=g¦————————-+————————-·t¦·————————-

           2         2      ƒ     2    

G(t):=g(0.9·t+1.6)·0.9

    €   1 ‚  €  1 ‚

I:=G¦-———-¦+G¦———-¦

      ‹3 ƒ   ‹3 ƒ

0.521149

Вычисление интеграла по квадратурной формуле наивысшей алгебраической степени точности оказалось в точности равным аналитически вычисленному интегралу.

Задача № 12: Погрешность формулы

Оценить погрешность вычисления определенного интеграла от функции   в пределах    по квадратурной формуле наивысшей  алгебраической степени точности, полученной в задаче № 10в, по сравнению  с аналитически точным. Проделать то же самое над усеченным степенным рядом, представляющим  , в который x входит со степенью не выше третьей.

Вычисление интеграла по квадратурной формуле

Преобразуем пределы интегрирования в канонические (задача №11) и вычислим значение интеграла от преобразованной функции по квадратурной формуле:

     €„            2         †      ‚

SOLVE¦¦0=a+b·(-1),——-·¹=a+b·1¦,[a,b]¦

     …            3         ‡      ƒ

„    ¹      ¹  †

¦ a=——-  b=——- ¦

…    3      3  ‡

       ¹     € ¹   ¹   ‚

S(t):=——-·SIN¦——-+——-·t¦

       3      3   3   ƒ

     €   1 ‚  €  1 ‚

Iq:=S¦-———-¦+S¦———-¦

       ‹3 ƒ   ‹3 ƒ

1.49226

Точное значение интеграла дает следующее:

 2/3·¹              

ˆ                   

‰      SIN(x) dx=1.5

 0                  

Найдем разложение функции синуса в ряд Тейлора, оставив в этом разложении слагаемые со степенями аргумента не выше 3:

                             3

                            x  

TAYLOR(SIN(x),x,0,3) = x - ———-

                             6

 2/3·¹                      

ˆ      €    3 ‚             

¦      ¦   x  ¦             

¦      ¦x-———-¦ dx = 1.39152

‰          6 ƒ             

 0                          

Отбрасывание членов ряда выше 3-й степени даст ошибку, которую можно вычислить, если проинтегрировать сумму из отброшенных членов ряда до, например, 13-го порядка:

 2/3·¹                                                

ˆ                                                     

‰      (TAYLOR(SIN(x),x,0,13)-TAYLOR(SIN(x),x,0,3)) dx

 0                                                    

0.108475