Информатика и выч. техника \ Программирование

Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 16

Вызвав и исполнив, например,  Rn(4) , получим

„ 1  0  1  1 †

¦ 0  1  0  1 ¦

¦ 1  0  1  0 ¦

¦ 1  1  0  1 ¦

… 1  1  1  0 ‡

Генерирование случайных векторов можно сразу же превращать в десятичные целые числа, суммируя весовые коэффициенты двоичных разрядов очередного вектора. Определение оператора с ядром Rn(i)¯i , генерирующим i-тый случайный вектор, который выполняет такое преобразование, выглядит следующим образом:

               € 4              k - 1         ‚

Rd(m) := VECTOR¦ ¤  (Rn(i))   ·2     , i, 1, m¦

               k=1        i,k                ƒ

Задавая целое число m в списке параметров имени, можно задать длину вектора с компонентами случайных целых чисел. Вызвав и исполнив, например,  Rd(17) , получим

[13, 10, 5, 11, 7, 15, 14, 12, 8, 1, 2, 4, 9, 3, 6, 13, 10]

К разряду условных операторов можно отнести непрерывные кусочно-ломаные функции:

SIGN(x) – функция знака, равная 1 при  x>0  и  -1  при  x<0;

STEP(x) – единичная функция, равная 1 при  x>0  и  0  при  x<0;

MAX(x1,x2,...,xn) – выделение максимального значения;

MIN(x1,x2,...,xn) – выделение минимального значения;

CHI(a,x,b) – функция равна 1, если  a < x < b  иначе – 0.

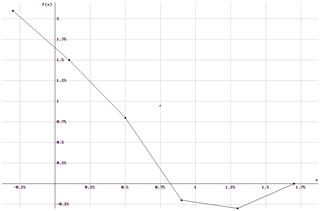
Например, на основе CHI() можно построить функцию, которая по таблично заданной функции строит кусочно-линейную кривую, то есть соединяет заданные точки отрезками прямых. Пусть задана таблица функции в виде матрицы W с двумя строками: W¯1 – абсциссы функции и W¯2 – ординаты:

 W :=„ -0.3  0.1  0.5   0.9   1.3  1.7 †

     …  2.1  1.5  0.8  -0.2  -0.3   0  ‡

Определение прямой линии, проходящей через две соседние точки заданной таблицы  (W¯1¯k, W¯2¯k)  и  (W¯1¯(k+1), W¯2¯(k+1)) имеет следующий вид:

           W       ·(W    - x) + W   ·(x - W       )

            2,k + 1   1,k         2,k       1,k + 1  

Fnk(W) := ———————————————————————————————————————————

                        W    - W                     

                         1,k    1,k + 1              

Умножив функцию прямой линии на единичный отрезок между точками  (k, k+1) и просуммировав такие произведения по всем интервалам, получим следующее определение кусочно-ломаной, параметром которой является имя таблично заданной функции W :

        DIMENSION(W™1) - 1                             

Lmn(W):=       ¤          Fnk(W)·CHI(W   , x, W       )

              k=1                     1,k      1,k + 1

Для построения графика функцию Lmn(W) обязательно надо исполнить, чтобы получить конкретное представление ломаной в функции одного аргумента. Количество слагаемых результата будет не менее числа интервалов в табличной функции:

            3·¦10·x - 17¦     ¦10·x - 13¦     9·¦10·x - 9¦  ~

Lmn(W):= - ——————————————— + ————————————— + —————————————— ~

                  80               20              80       ~

~   3·(11 - 10·x)·SIGN(10·x + 3)   ¦10·x - 1¦ + 15·¦2·x - 1¦

~ + ———————————————————————————— - —————————————————————————

~               40                              80          

Преобразование и декомпозиция выражений

Наиболее часто при выполнении символьных преобразований текущих выражений используют встроенные команды, вызываемые в пункте Simplify главного меню. Команды EXPAND(), APPROX(), FACTOR() являются к тому же операторами, которым можно по общим правилам дать имя со списком параметров для передачи их значений в преобразуемые выражения. Формат описаний таких операторов показан в следующих ниже строках, которые предназначены для преобразования некоторого выражения  Name(arg1, arg2):

EXPAND(Name(arg1, arg2), Trivial, arg1, arg2)

EXPAND(Name(arg1, arg2), Rational, arg1)

APPROX(Name(arg1, arg2), 25)

FACTOR(Name(arg1, arg2), Complex, arg1, arg2)

Первый оператор выполнит тривиальное разложение выражения  (раскрытие скобок) относительно двух аргументов  arg1,arg2 . Второй – выполнит то же самое, но составляющие выражения будут представляться в рациональной форме, как и при уставке Notation := Rational:

 Rd(5)

———————

   15  

„ 13    2    1    11     7 †

¦————, ———, ———, ————, ————¦

… 15    3    3    15    15 ‡

Скачать файл