Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 15

Например, функция  (SIN(x)·COS(y))^2  будет выглядеть так:

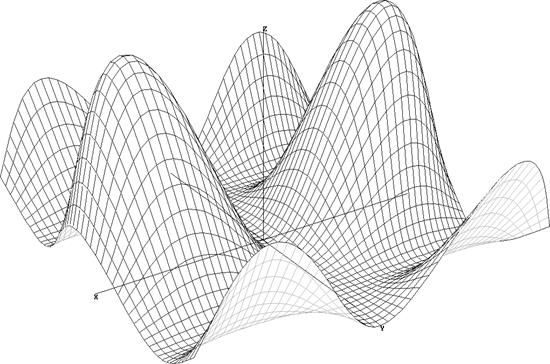
Ракурс изображения может быть подобран с помощью горячих кнопок. Ими же можно установить диапазон изменения каждой из трех переменных (x,y,z) и количество сечений по осям x и y.

Пакеты DERIVE версий 5.0 и выше позволяют выполнять больше манипуляций с изображением, в том числе и включать непрерывное вращение поверхности вокруг вертикальной оси z.

Условные операторы пакета DERIVE

Общая форма условного оператора представляется именем IF со списком параметров:

IF (test, then, else, unknown)

Фактическими параметрами могут служить выражения, функции, операторы. На месте формального параметра test помещают условное предложение, связывающее операциями отношений два выражения, формирующих значения одинакового типа. Если условие истинно, то выполняется оператор, поставленный на месте формального параметра then, если ложно, то выполняется оператор, поставленный на месте формального параметра else. При невозможности определения истинности (например, при несовпадении типов значений в условном выражении) выполняется оператор последнего параметра в списке.

Если отсутствует unknown, то при некорректности условия по умолчанию выводится знак вопроса ‘?’. Если присутствует лишь условное предложение, то оператор формирует значение равное 1, когда условие истинно, и равное 0, когда условие ложно, например, исполнение вектора с двумя условными компонентами  [IF(2 > 3), IF(2 < 3)]  дает результат  [0, 1].

Прочие несогласованности при опущенных параметрах выводят на обозрение строку условного оператора.

Условные предложения могут быть представлены в трех формах:

Ø  G(x) Ä H(y) – отношение с операторами арифметического типа, в котором операция отношения  ÄÎ{= | /= | < | <= | > | >=};

Ø  p Å q Å s – булевы функции с логическими переменными (p,q,s), принимающими значения true и false , и функционально полным базисным набором логических операций  ÅÎ{NOT | AND | OR};

Ø  p Å (G(x) Ä H(y))Å (q Å s) – смешанные выражения, содержащие как первые, так и вторые.

Записи смешанных выражений могут быть сведены к более простым, если их предварительно исполнить, например, запись в командной строке

6 >= -2·x AND 3·x /= -9

выведенная на экран монитора и исполненная даст следующее выражение:

6 ’ - 2·x  3·x ≠ -9     Þx > -3

Использование вложенных условных операторов покажем на примере генерирования матрицы, в которой строки представляют собой случайные векторы V, состоящие из элементов {0, 1}. В качестве датчика случайных векторов V используем образ 4-разрядного двоичного регистра сдвига с обратной связью, вдвигаемый слева первый разряд которого представляется результатом сложения по модулю 2 второго и четвертого разрядов. Операцию сложения по модулю два представим условной переменной tst1, определенной следующим образом:

tst1 := IF(V  = 0, IF(V  = 0, 0, 1), IF(V  = 0, 1, 0))

            4          2                 2            

Результатом исполнения этого выражения будет либо 0, либо 1. Вектор из случайных векторов V будем формировать с помощью оператора ITERATES() с векторными параметрами:

ITERATES(„tst1, V , V , V †, V, [1, 0, 1, 1], 5)

         …       1   2   3‡                     

Первой компонентой формируемого случайного вектора V поставлена переменная tst1, а следующие компоненты являются значениями соседних слева компонент исходного вектора, имитируя сдвиг содержимого регистра вправо. Начальным состоянием регистра взят вектор [1,0,1,1]. Исполнив этот оператор, получим матрицу:

„ 1  0  1  1 †

¦ 1  1  0  1 ¦

¦ 0  1  1  0 ¦

¦ 1  0  1  1 ¦

¦ 1  1  0  1 ¦

… 0  1  1  0 ‡

Если в качестве разрядов, суммируемых по модулю 2 использовать третий и четвертый, то результат можно определить так:

tst := IF(V  = 0, IF(V  = 0, 0, 1), IF(V  = 0, 1, 0))

           4          3                 3            

Матрице можно дать имя с параметром, определяющим количество строк:

Rn(m) := ITERATES(„tst, V , V , V †, V, [1, 0, 1, 1], m)

                  …      1   2   3‡