Не менее важным является и вопрос оценки границ диапазона, в котором находится нужное значение корня уравнения одной переменной. Для этих целей удобно использовать графические возможности DERIVE.
Построение графиков функций одной переменной возможен только для результатов выполненных операторов или процедур. Для перехода в графический режим необходимо выделить курсором функцию или функциональный фрагмент одной переменной в выражении какого-либо оператора или процедуры и нажать режимную (горячую) кнопку с изображением одномерного графика.
Например, после выделения в предыдущем примере правой части определения функции f(x) и нажатия режимной клавиши одномерного графика откроется графическое окно с прямоугольной системой координат со своими горячими кнопками.
Щелкнув мышкой по кнопке с аналогичным изображением одномерного графика, на экране монитора будет построен график соответствующей функции. Горячими кнопками или установками в главных и вспомогательных позициях меню можно добиться нужного формата и размера кривой. График выделенной функции имеет вид:
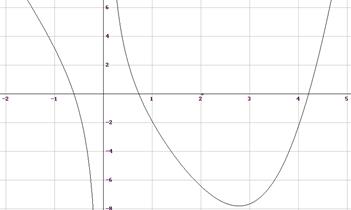
Для оператора SOLVE() по графику легко указать границы диапазонов, в которых находятся корни уравнения. Графики различных функций или функциональных фрагментов накладываются друг на друга в любом количестве, если предыдущие изображения их не удалять, например, горячей кнопкой с красным зачеркивающим крестиком.
Получаемые изображения можно передать в другие пакеты, поместив их в буфер. В буфер можно поместить все изображение переднего окна или его выделенную маркером часть. Выбор того или иного варианта определяется специальными позициями пункта Edit главного меню: Copy Window и Marc and Copy…
Для вывода семейства нескольких графиков функций за одно вхождение в графический режим необходимо все определения функций представить в алгебраическом окне элементами матрицы с одним столбцом и числом строк, соответствующим числу функций, например:
i
VECTOR(x , i, 0, 3)
2 3
1 x x x
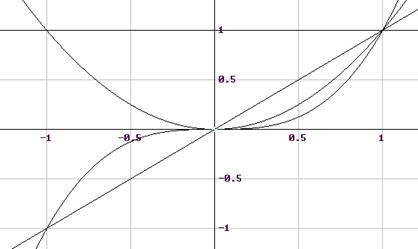
Если одномерная функция задана таблично и эта таблица представлена числовой матрицей, первый столбец которой представляет значение абсциссы, а второй – значение ординаты, то после выделения ее и перехода в одномерный графический режим можно нанести эти точки на поле графика.
[SIN(x), VECTOR([x, SIN(x)], x, 0, 1.2, 0.2)]
0 0
¦ ¦ 0.2 SIN(0.2·5) ¦¦
¦ ¦ 0.4 SIN(0.2·10) ¦¦
¦SIN(x), ¦ 0.6 SIN(0.2·15) ¦¦
¦ ¦ 0.8 SIN(0.4·5) ¦¦
¦ ¦ 1 SIN(1) ¦¦
1.2 SIN(0.2·30)
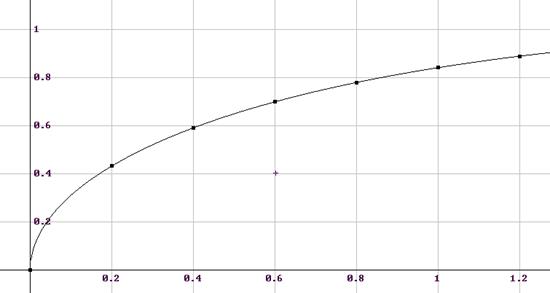
В этом фрагменте в квадратных скобках были перечислены одномерная функция и оператор формирования матрицы ее оцифровки. После исполнения этого блока на соответствующих местах исходного вектора оказались функция и ее табличное представление. Выделив курсором этот результат для отображения, получаем график с нанесенными на него точками из таблицы.
Управление внешним видом графика облегчается, если использовать горячие кнопки и курсорный крестик на графическом поле. Последний перемещается в нужное место клавишами со стрелками на клавиатуре или мгновенно – щелчком мыши по нужному месту. Этот курсор-крестик указывает на ту точку изображения, которое должно оказаться в центре экрана монитора, если щелкнуть по горячей кнопке, где точка размещена в центре кнопки. Если щелкнуть по кнопке, в центре которой помещено перекрестие координатной системы, то в центр экрана монитора смещается начало координатной системы изображаемых графиков.
Выделенное курсором определение функции двух переменных, можно представить поверхностью в трехмерной системе координат, если перейти в соответствующий графический режим, щелкнув мышкой по горячей кнопке с изображением трехмерной системы координат. Трехмерное графическое окно тоже имеет свое главное меню со своим набором горячих кнопок. Команда на построение поверхности поступает в момент нажатия своей кнопки с изображением трехмерной координатной системы. Построение очередной поверхности стирает предыдущее трехмерное изображение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.