Численные методы в среде символьной математики. Программирование и решение задач: Учебно-методическое пособие, страница 8

При наличии в конце имени буквы S результат формируется в виде (n+1)-мерного вектора V[i] из значений промежуточных подстановок, первым элементом которого является x0. При отсутствии S результатом выполнения оператора является значение последней n-й подстановки. Схема алгоритма показана на рисунке справа.

Итерации применяются в методах численного решения уравнений. Наиболее популярен метод Ньютона для поиска корней алгебраического уравнения вида . Формула итерационного (последовательного) приближения к корню    от заданного приближенного значения  имеет следующий вид:

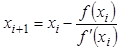    или    .

Для примера с помощью итерационного метода Ньютона найдем корень следующего уравнения:

 3      2           

x  - 8·x  - 5·x + 84 = 0.

В соответствии с формулой Ньютона составим функцию для итерационного приближения:

                 3      2              

                x  - 8·x  - 5·x + 84   

f(x) := x - ———————————————————————————

             d    3      2             

             —— (x  - 8·x  - 5·x + 84)

             dx                        

Для упрощения выражения выделим курсором только правую часть этого выражения и, обратившись к пунктам меню, сделаем нужные установки следующим образом:

SimplifyFactor ExpressionFactor Vareables: x Ù Amount: RationalОК

             3      2       

         2·(x  - 4·x  - 42)

f(x) := ————————————————————

              2             

           3·x  - 16·x - 5  

Введем эту функцию в список фактических параметров оператора итерационных подстановок. Укажем в нем количество подстановок равное 8. Начальное значение установим равным 16, в надежде найти максимальный по величине корень.

ITERATES(f(x), x, 16, 8)

[16, 11.95, 9.418, 7.944, 7.232, 7.020, 7.000, 7, 7]

Функция f(x) и ее аргумент x могут быть и векторами. Например, для получения ряда Фибоначчи, который определяется рекуррентной формулой, связывающей три его последовательных члена равенством вида

,

для начальных членов  и , в командной строке необходимо записать следующее выражение:

fib(n) := ITERATES([v™2, v™1 + v™2], v, [0, 1], n)

fib(n) := ITERATES(„v , v  + v †, v, [0, 1], n)

                   … 2   1    2‡               

Здесь вектор v представлен двумерным отрезком ряда (), начальное значение которого принято равным  () = (0, 1). Векторная функция перемещает второй элемент вектора на место первого элемента, а второй элемент заменяет суммой первого и второго. В результате оператором ITERATES() должен формироваться вектор с (n+1)-й компонентой, каждая из которых представляется двумерными векторами. Вызвав по имени этот оператор с n=5, получим результат, показанный справа.

Ниже приведены примеры формирования двух векторов: вектора с компонентами натурального ряда чисел и  вектора степеней переменной x .

n(x):=ITERATES(x+1,x,1,9)

[1,2,3,4,5,6,7,8,9,10]

º(x):=ITERATES(x·p,p,1,9)

„     2  3  4  5  6  7  8  9†

      …1,x,x ,x ,x ,x ,x ,x ,x ,x ‡

Пример подстановки векторного аргумента с использованием операторов из тематических утилит, то есть сгруппированных по темам процедур, записанных в форме программ на языке пакета DERIVE. Пусть необходимо численно проинтегрировать систему дифференциальных уравнений первого порядка методом Рунге-Кутта.

Утилита, включающая в себя подборку процедур численного интегрирования дифференциальных уравнений, имееет файловое имя ODE_APPR.mth. Загрузка утилиты в доступную для текущего сеанса область памяти, минуя выдачу всех текстов процедур на экран монитора в алгебраическое окно, осуществляется так:

FileLoadUtility…File name: ODE_APPR.mth Ù Open

Формат оператора, вызывающего процедуру Рунге-Кутта, имеет следующий вид: RK(u, v, v0, h, k). Формальные параметры процедуры включают: n-мерный вектор системы уравнений u, элементами которого являются правые части уравнений системы; (n+1)-мерный вектор имен искомых переменных v, первым элементом которого является имя независимой переменной; (n+1)-мерный вектор начальных значений переменных v0; шаг h по независимой переменной и число шагов k.