Нелинейная фильтрация сигналов: Учебное пособие, страница 8

3)  каким-либо образом дополняют исходный сигнал  значениями в начале и конце, одним из вариантов такого дополнения может быть "зеркальное", в соответствии с которым  и  для .

Несмотря на указанные выше способы возможного решения краевой задачи, получаемые значения  в начале и конце сигнала являются "искусственными", поэтому при анализе свойств фильтров не рекомендуется рассчитывать какие-либо количественные показатели эффективности фильтрации с учетом начальных и конечных отсчетов.   

Контрольные вопросы

1. Что такое скользящее окно и каковы его типичные размеры?

2. Что такое медиана выборки и как она рассчитывается?

3. Как бороться с краевыми эффектами?                   

4. УСТОЙЧИВЫЕ МЕТОДЫ ОЦЕНИВАНИЯ

Рассмотрим идеализированный случай, когда в пределах скользящего окна с центром в i-м отсчете все значения  одинаковы, но вследствие влияния помех наблюдаемые значения   различны и по этим значениям необходимо получить по возможности наиболее точную оценку . Тогда задача фактически аналогична задаче обработки многократных измерений постоянного параметра в целях получения его оценки. Известны [10] основные требования к оценкам параметров, получаемым по выборке Х₁,Х₂,...Х_Ns. В данном случае выборка состоит из значений :. Оценки должны обладать несмещенностью, эффективностью и состоятельностью.

 Желательно, чтобы математическое ожидание оценки равнялось оцениваемому параметру, т. е. чтобы . Тогда несмещенной называют оценку параметра , математическое ожидание которой равно оцениваемому параметру при любом объеме выборки. Соответственно смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру. Естественно, в качестве приближенных требуется брать оценки несмещенные, чтобы не делать систематической ошибки в сторону завышения или занижения.

Оценка  параметра q (например среднего) выборки данных называется состоятельной, если она стремится по вероятности к оцениваемому параметру при неограниченном возрастании числа опытов, т. е. 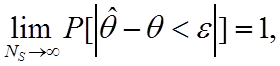 где e – сколь угодно малое положительное число. Для выполнения этого условия достаточно, чтобы дисперсия оценки стремилась к нулю при N_S ® ¥, т.е. чтобы выполнялось условие 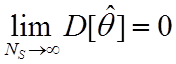 и оценка была несмещенной. Иными словами, состоятельность оценки означает, что при достаточно большом объеме выборки со сколь угодно большой достоверностью отклонение оценки от истинного значения параметра меньше любой заранее заданной величины.

Оценки, обладающие свойствами несмещенности и состоятельности, при ограниченном числе опытов могут отличаться дисперсиями. Чем меньше дисперсия оценки, тем меньше вероятность грубой ошибки при определении приближенного значения параметра. Эффективной называется оценка, которая при заданном объеме выборки имеет наименьшую возможную дисперсию среди всех возможных оценок.

При этом в выборке Х₁,Х₂,..,Х_Ns могут быть как достаточно точные (нормальные) измерения, так и аномальные (грубые погрешности).  Прежде всего отметим, что наличие в выборке Х₁,Х₂,...Х_Ns грубых погрешностей может быть обусловлено различными факторами, имеющими место в практике измерений (см. разд. 1).

         Ненулевая вероятность Р₀ появления в выборке грубых погрешностей (аномальных измерений) приводит к нескольким последствиям. Во-первых, закон распределения оценок параметра оказывается отличающимся от исходных предположений о нем. Для его описания часто используют модель составного распределения вида [12]                

p(x)=(1-P₀) p_осн(x) + P₀ p_загр(x),                              (10)

где p_осн(x) – плотность распределения вероятности основного распределения, которому подчиняются "нормальные" измерения;  p_загр(x) – плотность распределения вероятности так называемого загрязняющего распределения, описывающего статистические характеристики аномальных измерений (грубых погрешностей).