Нелинейная фильтрация сигналов: Учебное пособие, страница 2

Все фильтры, для которых может не выполняться условие , относятся к очень широкому классу нелинейных фильтров.

Перечислим некоторые другие отличия линейной и нелинейной фильтрации.

Во-первых, цифровая линейная фильтрация исторически развивалась как продолжение аналоговой линейной фильтрации по мере того, как цифровые устройства, ЭВМ и компьютеры с повышением их быстродействия позволяли реализовывать основные типы линейных фильтров (ФНЧ, ФВЧ, полосовые, режекторные, линейные адаптивные [12]) для все более высоких частот дискретизации сигналов и сложностей соответствующих алгоритмов. Нелинейная фильтрация фактически сразу, с начала своего развития, ориентировалась на использование цифровых устройств и компьютеров, поскольку аналоговая реализация многих нелинейных фильтров либо невозможна, либо сопряжена со значительными трудностями.

Во-вторых, определенные проблемы связаны с созданием обобщенной теории нелинейной фильтрации, а также анализом свойств и синтезом нелинейных фильтров. Для некоторых частных ситуаций (например, для рассмотренных ниже фильтров на порядковых статистиках) в качестве базового математического аппарата небезуспешно используются теория булевых функций, методы пороговой декомпозиции, а также теория вероятностей и робастных оценок. Вместе с тем вследствие сложности аналитического исследования свойств фильтров численное моделирование продолжает оставаться одним из основных средств анализа.

Кроме того, для алгоритмов цифровой нелинейной фильтрации в целом характерно более низкое быстродействие, чем для цифровых линейных фильтров. Однако главное отличие и преимущества нелинейных методов фильтрации сигналов состоят в том, что существует большое количество практических ситуаций, когда их применение по тем или иным причинам является более целесообразным, чем использование линейных фильтров. Напомним, что линейные фильтры разрабатываются (и в результате успешно применяются) при выполнении определенных предположений о характеристиках сигналов и помех. Основными из этих предположений являются временная стационарность, то есть неизменность во времени основных статистических и спектрально-корреляционных характеристик сигналов и помех, а также часто гауссов закон распределения шумов, подлежащих подавлению [11]. Однако на практике нередко одно или многие из этих предположений не выполняются.

Рассмотрим некоторые характерные практические ситуации. При этом отметим, что под цифровым сигналом ниже будем понимать не только собственно дискретизированный сигнал (последовательность отсчетов) , поступающий непосредственно от какого-либо датчика или с выхода приемного устройства и усилителя после аналого-цифрового преобразования этого сигнала (пример - электрокардиографические сигналы в медицине), но и последовательность , где  – i-я оценка некоторого изменяющегося во времени или пространстве параметра , полученная в результате выполнения первичной обработки принятых или зарегистрированных сигналов. Примером может служить последовательность оценок длительности ЭКГ-цикла (расстояния между R-зубцами) для тех же электрокардиографических сигналов, которая характеризует изменчивость сердечного ритма (рис. 1).

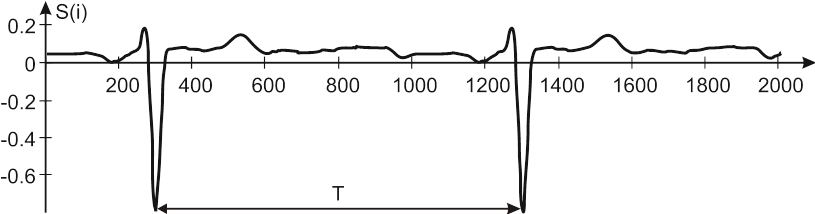
Рис. 1. Электрокардиографический сигнал (2 цикла)

Ситуация 1. Сигналы могут содержать резкие перепады, что характерно, например, для сигналов в цифровых системах управления, содержащих "скачки" значений, или для ЭКГ-сигналов (рис. 2, а, б, г). Отметим, что сигналы, показанные на рис. 2, часто используют в качестве эталонных для анализа и сравнения эффективности различных методов нелинейной фильтрации и широко используются специалистами, работающими в данной области.

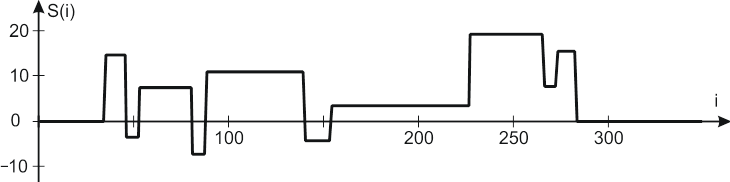
а

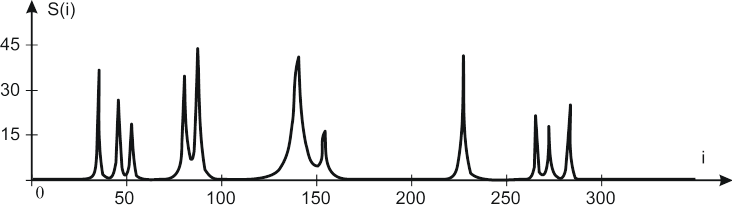
б

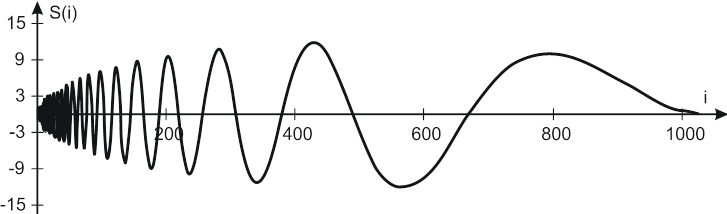
в

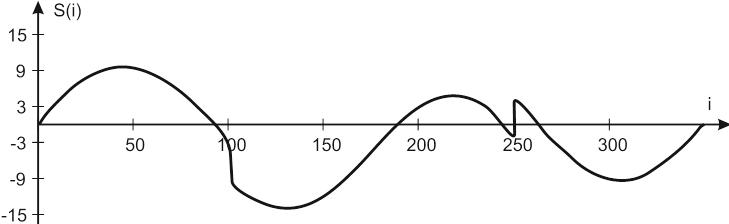
г

Рис. 2. Стандартные эталонные сигналы: Blocks (а); Bumps (б);

Doppler (в); HeavySine (г)