Нелинейная фильтрация сигналов: Учебное пособие, страница 25

19. Лукин В.В., Тулякова Н.О., Дорощук М.О. Анализ свойств алгоритмов нелинейной фильтрации одномерных информационных процессов // Авиационно-космическая техника и технология. – Х.: ХАИ. – 1999. - Вып. 12. - С. 109 - 113.

20. Лукин В.В., Абрамов С.К. Анализ характеристик выходных сигналов нелинейных фильтров при воздействии сложных помех // Сб. науч. ст. «Авиационно-космическая техника и технология». – Х.: ХАИ. – 1999. – Вып. 12. – С. 106 - 109.

ПРИЛОЖЕНИЕ

Примеры выходных сигналов различных нелинейных фильтров для тестового сигнала, показанного на рис. 8

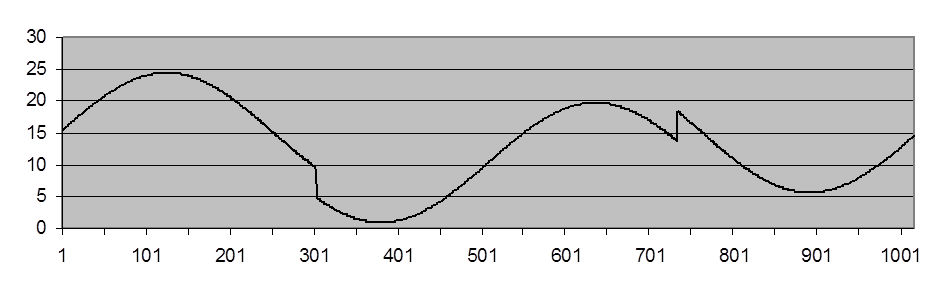
Рис. П.1. Тестовый сигнал без помех

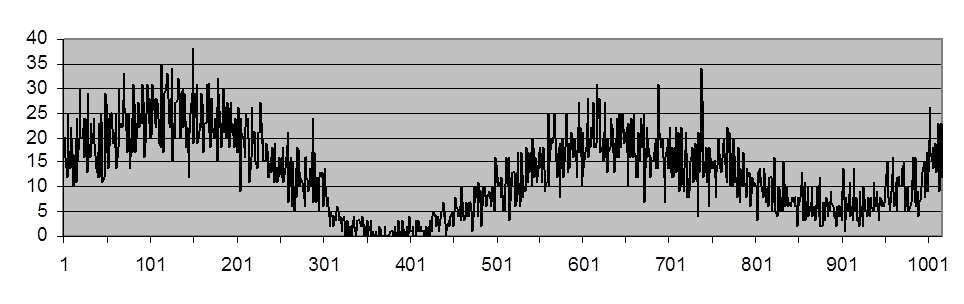
Рис. П.2. Тестовый сигнал, искаженный шумом с пуассоновской ПРВ (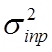=14,1)

         Данный тестовый сигнал обрабатывался различными фильтрами, но для всех из них размер скользящего окна был равен 9. Для всех полученных отфильтрованный сигналов рассчитывалось  для всего сигнала, а также локальная среднеквадратическая ошибка  в окрестности характерного отсчета с индексом 301, где имеет место «резкий перепад» значений сигнальной составляющей. Полученные значения  и  приведены под соответствующими графиками выходных сигналов, там же дан краткий анализ некоторых свойств рассматриваемых неадаптивных фильтров.

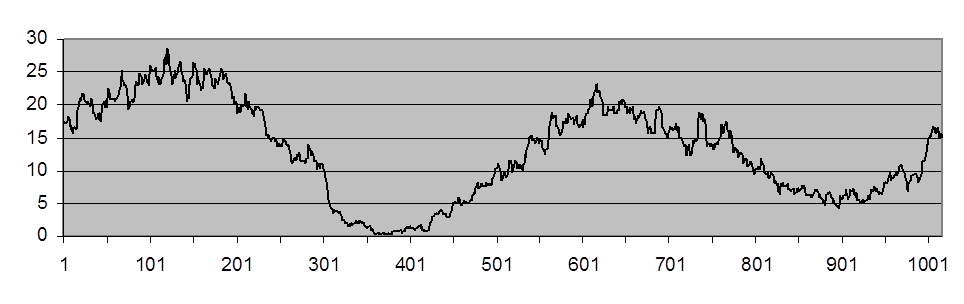 Рис. П.3. Выходной сигнал линейного усредняющего фильтра (=1,60 и =2,19)

         Как видно, имеет место эффективное подавление помех, но в окрестностях 301-го и 740-го отсчетов «резкий перепад» и «ступенька» существенно смазаны.

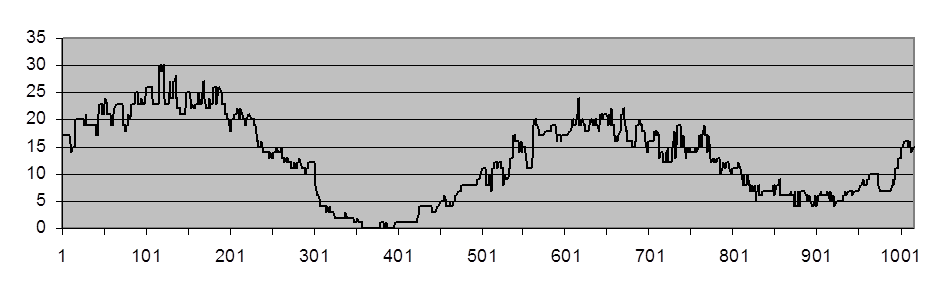
Рис. П.4. Выходной сигнал стандартного медианного фильтра

( = 2,87 и  = 2,41)

Перепад в окрестности 301-го отсчета визуально сохранен лучше, но по количественным критериям  и  СМФ уступает ЛУФ. Кроме того, имеются участки постоянных значений выходного сигнала. Это связано с тем, что выходным значением СМФ может быть только одно из значений, содержащихся в выборке для данного положения скользящего окна, причем для нескольких соседних положений скользящего окна медианой может оказаться одно и то же значение.  

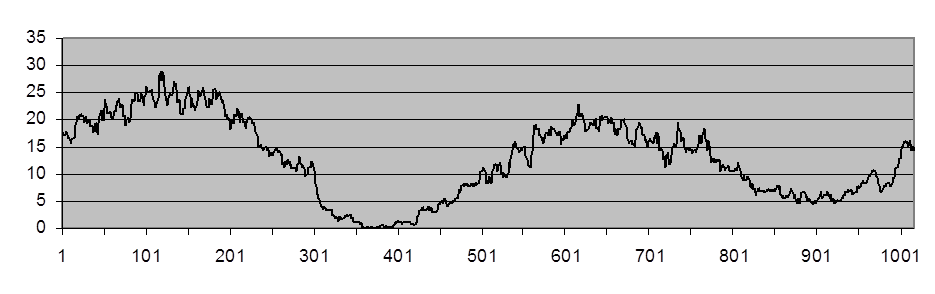
Рис. П.5. Выходной сигнал a-урезанного фильтра с N_a=2

( = 1,93 и  = 2,53)

АУФ занимает промежуточное место между ЛУФ и СМФ по своим основным свойствам, т.е. подавляет помехи чуть лучше и сохраняет перепады чуть хуже, чем СМФ.

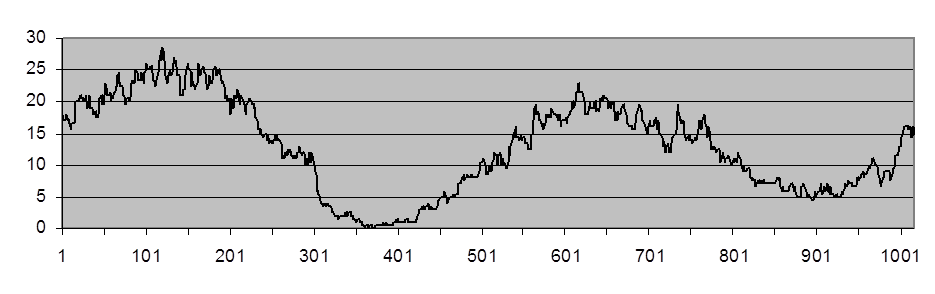
Рис. П.6. Выходной сигнал фильтра Вилкоксона

(=1,72 и =2,14)

Выходной сигнал фильтра Вилкоксона по своим основным свойствам близок к ЛУФ, но, в отличие от ЛУФ, ФВ способен устранять импульсные помехи.

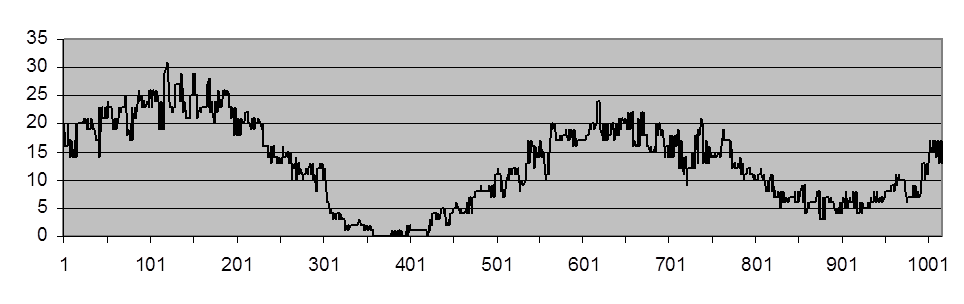 Рис. П.7. Выходной сигнал центрально-взвешенного медианного фильтра с весом центрального элемента, равным 3

( = 3,76 и  = 3,13)   

Центрально-взвещенный медианный фильтр по своим свойствам близок к СМФ, но хуже его подавляет шум.

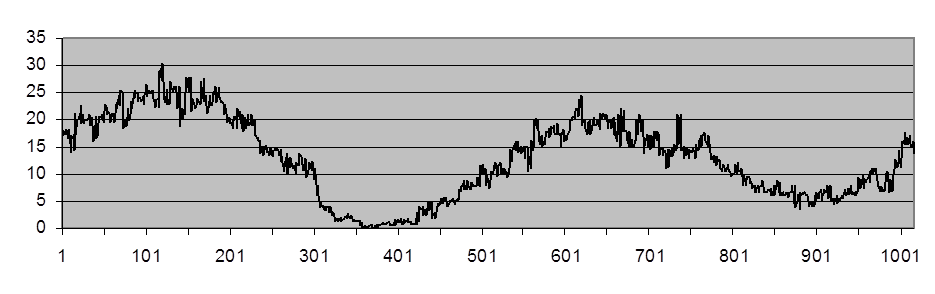
Рис. П.8. Выходной сигнал КИХ-гибридного медианного фильтра

( = 2,49 и  = 2,54)

Выходной сигнал КИХ-гибридного медианного фильтра по своим свойствам близок к СМФ, но чуть лучше его подавляет шум, при этом более чувствителен к импульсным помехам.

         При выборе относительно малого k мириадный фильтр плохо подавляет интенсивный флуктуационный шум (см. рис. П.9).

         По мере роста k мириадный фильтр по своим свойствам постепенно приближается к ЛУФ (см. рис. П.10 и П.11).

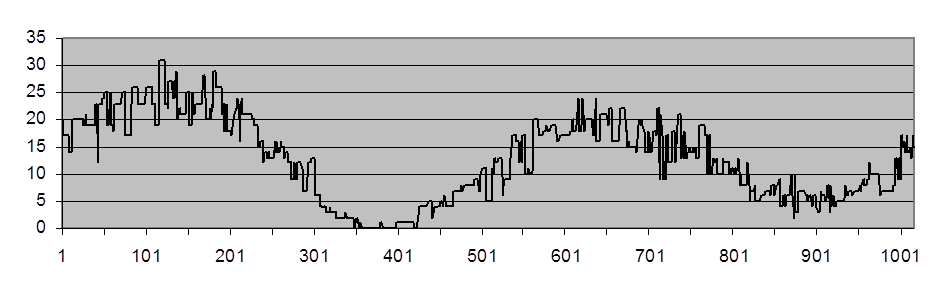
Рис. П.9. Выходной сигнал мириадного фильтра с k=0,1

( = 5,92 и  = 6,26)

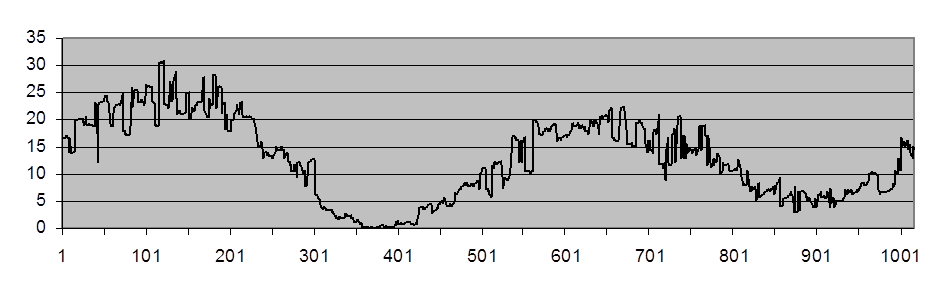
Рис. П.10. Выходной сигнал мириадного фильтра с k=1,0

( = 4,47 и  = 4,65)

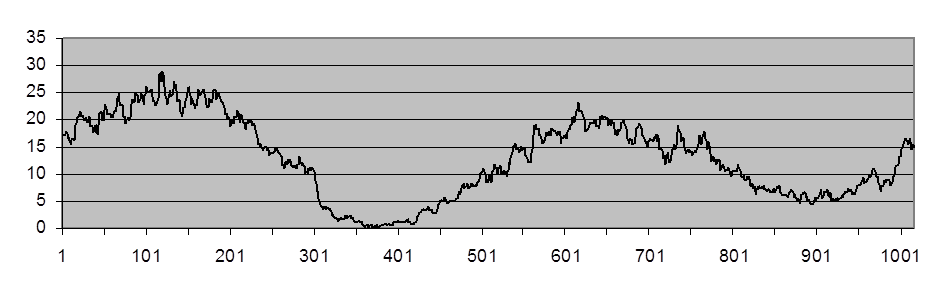
Рис. П.11. Выходной сигнал мириадного фильтра с k=10

( = 1,69 и  = 2,23)