Более подробный анализ приведен в работах [18, 19]. Показано, что некоторые КГМФ способны обеспечивать еще меньший уровень вносимых искажений, чем СМФ. Однако и приведенные данные в достаточной степени свидетельствуют о том, что при использовании для обработки сигналов и процессов нелинейных фильтров необходимо знать и иметь в виду те специфические искажения, которые они вносят в окрестностях характерных фрагментов сигнальной составляющей. Кроме того, следует учитывать, что в отличие от линейных фильтров для нелинейных вносимые искажения зависят от характеристик помех (см. разд. 8).
В заключение отметим, что специалисты, хорошо
знакомые с теорией и практикой линейной фильтрации, но редко сталкивающиеся со
спецификой нелинейной фильтрации, часто задают вопрос: являются ли нелинейные
фильтры в скользящем окне ФНЧ или ФВЧ? Такая постановка вопроса – исходно некорректна.
Попытки анализировать свойства нелинейных фильтров, используя подходы, традиционные
для теории линейной фильтрации, подробно рассмотрены в [2, 4]. Так, если
определять частотную передаточную функцию фильтра в виде 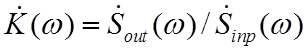 , где
, где 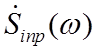 и
и ![]() - комплексные спектры соответственно
входного и выходного сигналов, то для нелинейных фильтров
- комплексные спектры соответственно
входного и выходного сигналов, то для нелинейных фильтров ![]() оказывается существенно отличающейся для
разных входных сигналов. Действительно, СМФ хорошо подавляет некоррелированный
шум на участке сигнала постоянного уровня и в этом плане он подобен ФНЧ. А в
плане сохранения резких перепадов некоторые нелинейные фильтры (например,
обычный медианный, центрально-взвешенный медианный, КИХ-гибридный медианный и
т.д.) как бы имеют
оказывается существенно отличающейся для
разных входных сигналов. Действительно, СМФ хорошо подавляет некоррелированный
шум на участке сигнала постоянного уровня и в этом плане он подобен ФНЧ. А в
плане сохранения резких перепадов некоторые нелинейные фильтры (например,
обычный медианный, центрально-взвешенный медианный, КИХ-гибридный медианный и
т.д.) как бы имеют 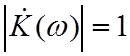 в бесконечно широкой полосе частот.
В то же время СМФ и другие нелинейные фильтры могут существенно искажать
сигнал, содержащий высокочастотную компоненту (пример – начальный участок
тестового сигнала на рис. 2, в).
в бесконечно широкой полосе частот.
В то же время СМФ и другие нелинейные фильтры могут существенно искажать
сигнал, содержащий высокочастотную компоненту (пример – начальный участок
тестового сигнала на рис. 2, в).
Контрольные вопросы
1. Для каких фрагментов сигналов нелинейные фильтры вносят наиболее существенные искажения?
2. Какие фильтры вносят наименьшие искажения?
3. Можно ли характеризовать нелинейные фильтры передаточной функцией?
8. ДИНАМИЧЕСКИЕ И СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ ФИЛЬТРОВ
Одним из способов описания и анализа динамических свойств фильтров является использование функций
![]() ,
(31)
,
(31)
описывающих
динамические ошибки на выходе фильтра, где Е означает усреднение по
ансамблю реализаций шума. Проблема анализа ![]() для
нелинейных фильтров состоит в том, что вид этой функции при фиксированной
сигнальной составляющей и заданном типе фильтра зависит от статистических
характеристик помех. Если для линейных фильтров при равенстве нулю
математического ожидания помех выполняется равенство
для
нелинейных фильтров состоит в том, что вид этой функции при фиксированной
сигнальной составляющей и заданном типе фильтра зависит от статистических
характеристик помех. Если для линейных фильтров при равенстве нулю
математического ожидания помех выполняется равенство
![]() ,(32)то есть
,(32)то есть ![]() не
зависит от, например, дисперсии помех, то для нелинейных фильтров это условие
не выполняется.
не
зависит от, например, дисперсии помех, то для нелинейных фильтров это условие
не выполняется.
Чтобы
убедиться в этом, достаточно рассмотреть функции ![]() в
окрестностях особых точек тестовых сигналов, исследованных в предыдущем
разделе, в случае воздействия гауссова «белого» шума с
в
окрестностях особых точек тестовых сигналов, исследованных в предыдущем
разделе, в случае воздействия гауссова «белого» шума с ![]() .
При этом «резкий перепад» описывается выражением
.
При этом «резкий перепад» описывается выражением 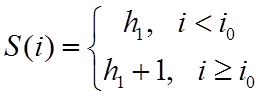 ,
,![]() , ломаная – выражением
, ломаная – выражением 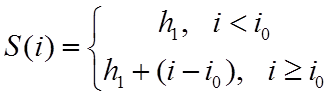 ,
,![]() , а полиномиальный
экстремум –
, а полиномиальный
экстремум –![]() ,
,![]() .
.
На
рис. 13 изображен график ![]() для окрестности резкого
скачка. Первое, что необходимо отметить, – это наличие динамической ошибки на
выходе СМФ.
для окрестности резкого
скачка. Первое, что необходимо отметить, – это наличие динамической ошибки на
выходе СМФ. ![]() на выходе СМФ меньше, чем для АУФ и ФВ, но
все же достаточно велика. При этом поведение
на выходе СМФ меньше, чем для АУФ и ФВ, но
все же достаточно велика. При этом поведение ![]() для
СМФ, а также других фильтров для рассматриваемого фрагмента зависит от
для
СМФ, а также других фильтров для рассматриваемого фрагмента зависит от ![]() и амплитуды (разности значений
и амплитуды (разности значений ![]() ) «резкого перепада».
) «резкого перепада».
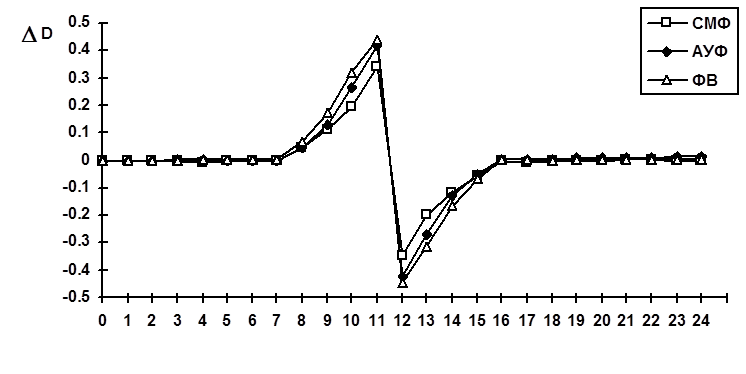
Рис. 13. Динамические ошибки в окрестности «резкого перепада»
На рис. 14 показаны динамические ошибки для сигнала «ломаная». Как и в предыдущем случае, наибольшие (по модулю) ошибки имеют место для выходных сигналов ФВ, чуть меньше – для АУФ, еще меньше – для СМФ.
Вновь вследствие присутствия помех на выходе СМФ наблюдаются динамические ошибки, хотя при отсутствии шума данный сигнал является стабильной точкой СМФ.
Для
третьего тестового сигнала – окрестности экстремума, описываемого полиномом
второго порядка, – графики ![]() представлены на рис.
15. Обратите внимание на особенность поведения динамической ошибки для ФВ (три
максимума) в сравнении с
представлены на рис.
15. Обратите внимание на особенность поведения динамической ошибки для ФВ (три
максимума) в сравнении с ![]() для СМФ и АУФ (один
максимум для
для СМФ и АУФ (один
максимум для ![]() ).
).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.