Слово ²устранять² часто употребляется в литературе, связанной с устойчивыми методами оценивания, для того, чтобы привлечь внимание к их преимуществам. Это слово взято в кавычки по следующим причинам. Устойчивые методы оценивания лишь заметно уменьшают негативное влияние «грубых погрешностей», содержащихся в выборке данных, на конечный результат обработки, но не ликвидируют это влияние полностью. Для анализа этих эффектов служат функции влияния [12]. Отметим, что при фиксированном P0 наиболее негативное влияние выбросов на статистические характеристики L- и R-оценок обычно наблюдается тогда, когда все или большинство выбросов имеют одинаковый знак. Кроме того, для большинства L- и R-оценок характерна тенденция возрастания степени негативного влияния выбросов по мере увеличения их отличия от истинного значения оцениваемого параметра, хотя, начиная с некоторого момента, при дальнейшем увеличении этого отличия степень негативного влияния выбросов мало изменяется.
Наряду с полезными результатами применение L- и R-оценок может приводить и к некоторым нежелательным эффектам. Так, для распределений, несимметричных относительно среднего, математические ожидания этих оценок могут не совпадать со средним значением. Например, для релеевского распределения математические ожидания медианы и оценки Вилкоксона отличаются от среднего в меньшую сторону. Аналогичные эффекты наблюдаются и в тех случаях, когда несимметричный вид имеет p(x) (10). Отмеченные особенности не умаляют преимущества устойчивых оценок, но требуют их аккуратного применения на практике.
М-оценкой, или
оценкой максимального правдоподобия, называется оценка Т, применяемая к
выборке Х1,Х2,..., ![]() , содержащей NS
элементов, которая определяется как решение экстремальной задачи (поиска
минимума) вида
, содержащей NS
элементов, которая определяется как решение экстремальной задачи (поиска
минимума) вида 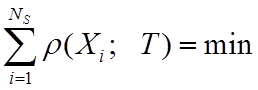 или как решение
неявного уравнения
или как решение
неявного уравнения 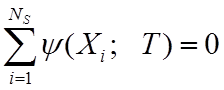 , где
, где ![]() –
произвольная функция,
–
произвольная функция, ![]() . Медиане соответствуют функции
. Медиане соответствуют функции ![]() и
и ![]() , где sgn() –
знаковая функция, равная нулю для нулевого аргумента, 1 для положительного аргумента
и –1 для отрицательного.
, где sgn() –
знаковая функция, равная нулю для нулевого аргумента, 1 для положительного аргумента
и –1 для отрицательного.
За
счет выбора определенных видов функций ![]() и
и ![]() можно варьировать свойства М-оценок и, в
частности, добиваться их устойчивости к выбросам. Одной из таких оценок является
мириада, формальное описание которой имеет вид
можно варьировать свойства М-оценок и, в
частности, добиваться их устойчивости к выбросам. Одной из таких оценок является
мириада, формальное описание которой имеет вид 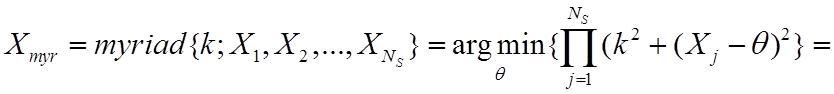
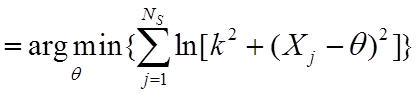 , где
, где ![]() –
настроечный параметр. Отметим, что мириадная оценка является оптимальной
(эффективной оценкой) для распределения Коши, часто используемого для моделирования
помех и процессов с высокой импульсивностью.
–
настроечный параметр. Отметим, что мириадная оценка является оптимальной
(эффективной оценкой) для распределения Коши, часто используемого для моделирования
помех и процессов с высокой импульсивностью.
Свойства
мириадной оценки существенно зависят от параметра k.
Свойство модальности, т.е. способности мириады определять координату моды
(области наибольшей концентрации значений измерений в выборке или максимума
ПРВ), которое весьма полезно для случаев несимметричной плотности распределения
p(x)
(10),
наблюдается при относительно малых k.
При относительно больших k свойства
мириады близки к свойствам оценки среднего выборки. Характерно, что для
относительно малых k
мириада выборки становится все менее чувствительной к наличию в выборке
выбросов при увеличении отличия «грубой погрешности» от истинного значения измеряемого
параметра. Таким образом, имеется возможность варьировать в широких пределах
свойства мириадной оценки. Однако для надлежащей установки k
необходимо априорно знать или предварительно определять масштаб данных.
Например, для pосн(x) в
(10)
модальный режим работы мириады имеет место при k<
2![]() . Напомним, что и для методов устранения
«грубых погрешностей» [15] необходимо априорное знание или предварительное
определение среднеквадратического отклонения или дисперсии. Однако при наличии
в выборке «грубых погрешностей» обычные (неробастные) методы оценивания СКО
дают сильно искаженные результаты. В связи с этим разработаны методы устойчивого
оценивания масштаба данных, например:
. Напомним, что и для методов устранения
«грубых погрешностей» [15] необходимо априорное знание или предварительное
определение среднеквадратического отклонения или дисперсии. Однако при наличии
в выборке «грубых погрешностей» обычные (неробастные) методы оценивания СКО
дают сильно искаженные результаты. В связи с этим разработаны методы устойчивого
оценивания масштаба данных, например:
1)
абсолютное
медианное отклонение, которое рассчитывается следующим образом: 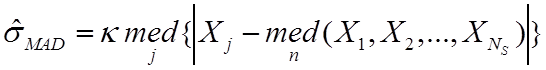 , где параметр
, где параметр ![]() выбирается
с учетом pосн(x), в
частности, для гауссовой pосн(x)
имеем
выбирается
с учетом pосн(x), в
частности, для гауссовой pосн(x)
имеем 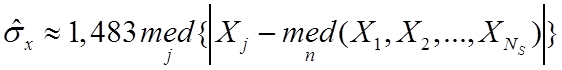 ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.