Нелинейная фильтрация сигналов: Учебное пособие, страница 4

Рис. 6. Тестовый сигнал без помех (а) и временная реализация этого сигнала, искаженного аддитивным шумом с дисперсией 0,001 и

импульсной помехой с  =1,0 и =0,03

Ситуация 3. Импульсные помехи (аномальные измерения) могут отсутствовать, но статистические характеристики шума или ошибок измерений могут быть сигнально-зависимыми или просто изменяющимися во времени. Приведем несколько типичных примеров.

Принцип работы некоторых датчиков состоит в том, что в течение временного интервала заданной длительности считается количество событий, например, импульсов для радиационных датчиков или изменений частоты (фазы) для систем обработки частотно- или фазоманипулированных сигналов. При этом для однократных измерений имеет место помеха с ПРВ по  Пуассону, описываемая в виде

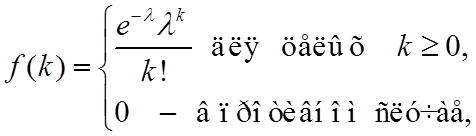                          (2)

где l – среднее число событий, удовлетворяющее условию . Пример такого процесса (последовательности измерений при постоянном ) показан на рис. 7. Специфика случайных величин, подчиняющихся ПРВ Пуассона, состоит также в том, что они принимают только целые значения и их ПРВ несимметрична относительно математического ожидания, равного l. Кроме того, дисперсии и,  соответственно, среднеквадратическое отклонение (СКО) зависят от математического ожидания (дисперсия равна l, а СКО – ).

Таким образом, если  изменяется во времени, то изменяется и дисперсия ошибок измерений.

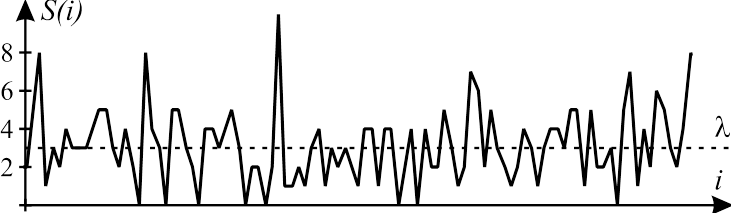
Рис. 7. Процесс с пуассоновским законом распределения

при постоянном   

Тогда более удобная модель представления наблюдаемого процесса  описывается выражением

     ,                                (3)

где  характеризует мультипликативные или сигнально-зависимые помехи (ошибки измерений) и имеет математическое ожидание, равное единице, и статистические характеристики (закон распределения, дисперсию и т.д.), зависящие в общем случае от . Пример такого процесса, для которого  представляет собой сигнал (см. рис. 2, г) с добавленной к нему постоянной составляющей (см. рис. 8, а), а мультипликативная помеха имеет дисперсию, пропорциональную , приведен на рис. 8, б. На рисунке хорошо видно, что интенсивность флуктуаций изменяется в зависимости от .

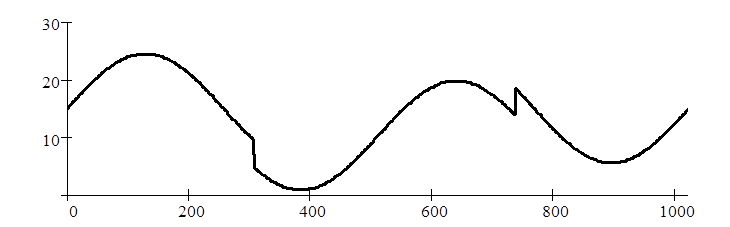
а

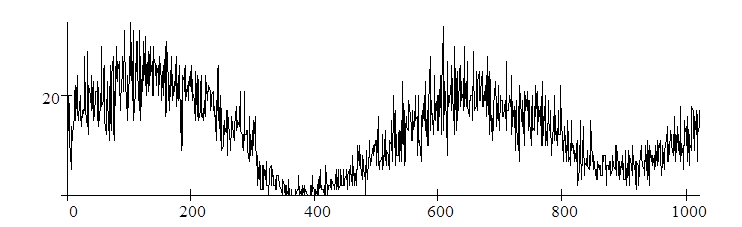
б

Рис. 8. Тестовый сигнал (а), искаженный сигнально-зависимой

помехой (б)

Одним из основных факторов, определяющих точность оценок параметров (обычно характеризуемую дисперсией этих оценок) в радиотехнических и других информационно-измерительных системах является соотношение сигнал–шум  на входе системы [5]. Однако это соотношение может изменяться во времени. Например, для систем радиолокации движущихся объектов или траекторных измерений, определяющих параметры траектории движения объектов (координаты и их производные),  зависит от расстояния до объекта. Это расстояние, очевидно, не остается постоянным в процессе слежения. Следовательно, имеет место нестационарность статистических характеристик . В этом случае статистические характеристики  в выражении  зависят от измеряемого параметра q (например угловых координат) или, в общем случае, от вектора параметров , характеризующих объект, для которого выполняется измерение его параметров.      

         На практике могут иметь место и другие комбинации свойств сигналов и помех. Тогда используются более сложные модели, чем (1) или (3). Однако для дальнейшего анализа важно следующее:

1)  для многих практических приложений имеет место нестационарность характеристик сигналов и помех;

2)  имеется острая необходимость фильтровать наблюдаемые процессы в целях либо получения оценки 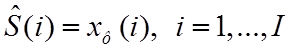, которая была бы более близкой к , чем наблюдаемый на фоне помех сигнал , либо для формирования более точных оценок некоторых параметров информационной составляющей .  

Необходимо иметь в виду, что любая фильтрация (линейная или нелинейная) наряду с полезным эффектом подавления помех неизбежно приводит к определенным искажениям, зависящим как от свойств и параметров сигнальной и помеховой составляющих, так и от свойств и параметров используемого фильтра. При некоторых, обычно очень больших, соотношениях сигнал–помеха на входе фильтра 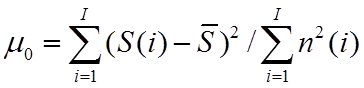, где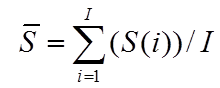, применение фильтра может привести к увеличению среднеквадратической ошибки на его выходе