Нелинейная фильтрация сигналов: Учебное пособие, страница 22

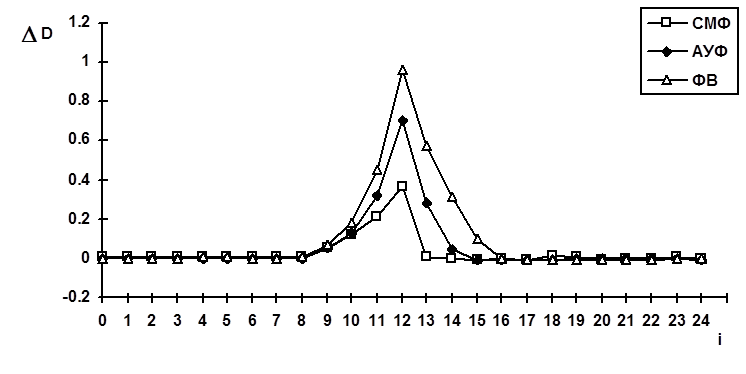
Рис. 14. Динамические ошибки в окрестности узловой точки ломаной

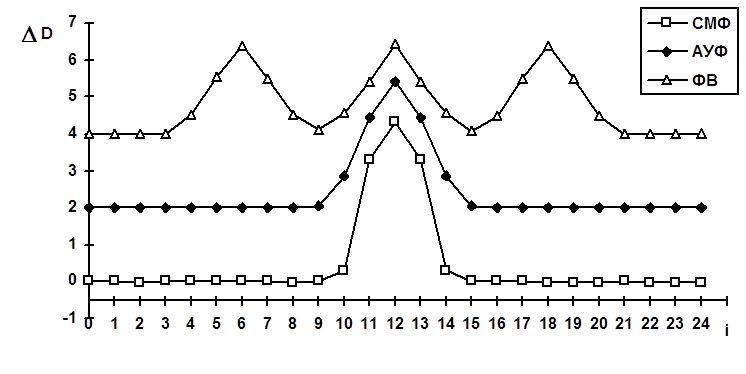
Рис. 15. Динамические ошибки в окрестности полиномиального

экстремума

         Основные выводы по результатам представленных и проведенных в [18] исследований динамических ошибок состоят в следующем:

1.  Даже если фрагмент сигнальной составляющей обрабатываемого процесса является стабильной точкой данного фильтра, то при воздействии помех может иметь место динамическая ошибка на его выходе.

2.   При возрастании дисперсии помех динамическая ошибка (по модулю) также увеличивается.

3.  По мере возрастания  преимущества нелинейных фильтров в плане сохранения характерных фрагментов сигнальной составляющей становятся все менее явно выраженными.

4.  Динамические ошибки весьма сложно описать аналитически вследствие их сложной зависимости от поведения сигнальной составляющей и характеристик помех. Лишь для нелинейных фильтров, свойства которых достаточно близки к свойствам ЛУФ, в частности для ФВ и АУФ при , можно в первом приближении использовать следующие выражения:

                                              ;            (33)

                                                ,              (34)

где ,  и  – соответственно динамические ошибки выходных сигналов АУФ, ФВ и ЛУФ при одинаковых N.

Для СМФ, КГМФ, ЦВМФ сложно получить такие обобщающие формулы, поскольку свойства этих фильтров являются очень нелинейными. К тому же, выражения (33) и (34) неприменимы при воздействии импульсных помех. Тем не менее эти приближенные формулы могут быть полезны для предсказания уровня динамических ошибок АУФ и ФВ, поскольку для ЛУФ имеется возможность аналитически оценить вносимые искажения либо интегрально (при заданном спектре сигнальной составляющей), либо локально, если сигнальная составляющая описана аналитически.

         Выше было сказано, что большинство нелинейных фильтров не вносят динамические ошибки для участков постоянного сигнала или линейно изменяющейся S(i), если шум n(i) имеет нулевое математическое ожидание и ПРВ, близкое к гауссовой (в принципе, главное, чтобы эта ПРВ была симметричной относительно нуля). Однако если последовательность {S(i)} искажена смешанным шумом (1), то даже при выполнении указанных выше предположений о ПРВ флуктуационной составляющей шума динамические ошибки  наблюдаются для окрестностей отсчетов, искаженных импульсными помехами [20].

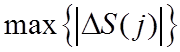         При этом ширина области, для которой, имеет порядок от примерно  до, а модульное значение ошибки – от величин, сравнимых с , до , где , ,  – индекс отсчета, искаженного импульсной помехой с .

         Чтобы проиллюстрировать этот эффект, рассмотрим следующий пример. Пусть для фрагмента наблюдаемого квантованного процесса . В табл. 5 приведены значения S(i), x(i), n(i), а также выходные значения СМФ с N = 5 и 7. Обратите внимание на тот факт, что  для i=6, 7 и 8, а  для i = 6, 7, 8 и 9. Это и есть искажения, обусловленные присутствием импульсной помехи в отсчете с .

Таблица 5

Выходные сигналы СМФ для линейно изменяющегося сигнала

	1	2	3	4	5	6	7	8	9	10	11	12	13
S(i)	5	10	15	20	25	30	35	40	45	50	55	60	65
n(i)	1	0	2	-1	1	25	0	-1	-2	1	0	2	-2
x(i)	6	10	17	19	26	55	35	39	43	51	55	62	63
xСМФ5(i)	-	-	17	19	26	35	39	43	43	51	55	-	-
xСМФ7(i)	-	-	-	19	26	35	39	43	51	51	-	-	-