В связи с наличием в рассмотренных выше сигналах «резких перепадов» и других характерных точек их спектры являются неограниченными. Более того, текущие спектры для различных фрагментов этих сигналов существенно отличаются. Этот эффект наблюдается и для тестового сигнала Doppler (рис. 2, в), хотя он и не имеет разрывов. Вместе с тем эти тестовые сигналы соответствуют многим типичным ситуациям в различных радиотехнических, коммуникационных и информационно-измерительных системах.
Ситуация
2. Помехи, которыми искажен сигнал, могут иметь явно выраженный негауссов
характер. Причины весьма разнообразны, поэтому сложно перечислить все возможные
эффекты и факторы, которые могут приводить к негауссову распределению помех ![]() или ошибок измерения
или ошибок измерения 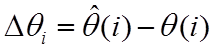 в случае, если обрабатываемая
последовательность
в случае, если обрабатываемая
последовательность ![]() . Некоторые причины негауссовости
ошибок измерений и помех перечислены ниже.
. Некоторые причины негауссовости
ошибок измерений и помех перечислены ниже.
Во-первых, измерения могут выполняться при малом соотношении сигнал–помеха. При этом меньшим соотношениям сигнал-помеха на входе измерительного устройства (системы или блока первичной обработки сигналов) соответствует большая вероятность Р0 появления в выборке грубых погрешностей.
Во-вторых, измерения могут производиться в одном или нескольких местах (пространственно разнесенными датчиками или устройствами), а затем по линиям связи передаваться (обычно уже в цифровом виде) на единый пункт сбора и обработки измерительной информации. В таких ситуациях вследствие тех или иных причин возможны ошибки кодирования/декодирования. При этом неправильное декодирование, особенно одного из старших разрядов в передаваемом числе, приводит к существенному искажению значения, в результате чего получаемое измерение с большой вероятностью становится аномальным (грубой погрешностью).
В-третьих, часто используемое предположение о гауссовом характере помех, искажающих сигнал, является идеализацией. В настоящее время для систем связи и мультимедийных средств более адекватными считают использование плотности распределения вероятности (ПРВ) помех с более «тяжелыми хвостами», чем для гауссовой ПРВ, например, симметричных a-стабильных (рис. 3).
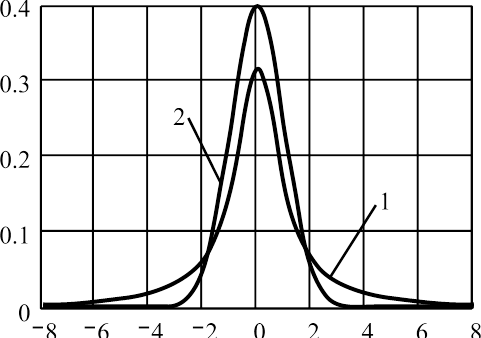
Рис. 3. ПРВ для нормального распределения (2) и распределения Коши (1), относящегося к симметричным a-стабильным
распределениям (a=1)
В
качестве другого примера приведем плотности распределения вероятности ошибок
измерения взаимной задержки ![]() случайных
широкополосных сигналов, принимаемых на фоне интенсивных аддитивных гауссовых
помех интерферометрической системой, при разных отношениях сигнал–помеха
случайных
широкополосных сигналов, принимаемых на фоне интенсивных аддитивных гауссовых
помех интерферометрической системой, при разных отношениях сигнал–помеха ![]() на входе приемников (рис. 4). По мере
уменьшения
на входе приемников (рис. 4). По мере
уменьшения ![]() возрастает вероятность
появления аномальных измерений и распределение
возрастает вероятность
появления аномальных измерений и распределение ![]() все в большей степени
отличается от гауссова.
все в большей степени
отличается от гауссова.
Для
сигналов, поступающих непосредственно от датчика или с выхода приемника,
аддитивная компонента помех ![]() также может
представлять собой сумму флуктуационной составляющей с законом распределения,
близким к гауссову, и импульсных помех, которые во многом аналогичны по своему
проявлению аномальным ошибкам измерений (выбросам). В этом случае более
корректная модель наблюдаемого процесса описывается выражением
также может
представлять собой сумму флуктуационной составляющей с законом распределения,
близким к гауссову, и импульсных помех, которые во многом аналогичны по своему
проявлению аномальным ошибкам измерений (выбросам). В этом случае более
корректная модель наблюдаемого процесса описывается выражением
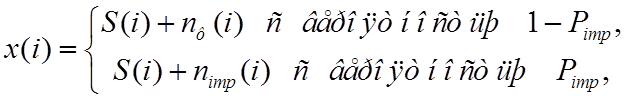 (1)
(1)
где ![]() – флуктуационная
составляющая шума (ошибка нормальных измерений),
– флуктуационная
составляющая шума (ошибка нормальных измерений), ![]() –
амплитуда импульсной помехи (аномальной ошибки), возникающей с вероятностью
–
амплитуда импульсной помехи (аномальной ошибки), возникающей с вероятностью![]() .
.
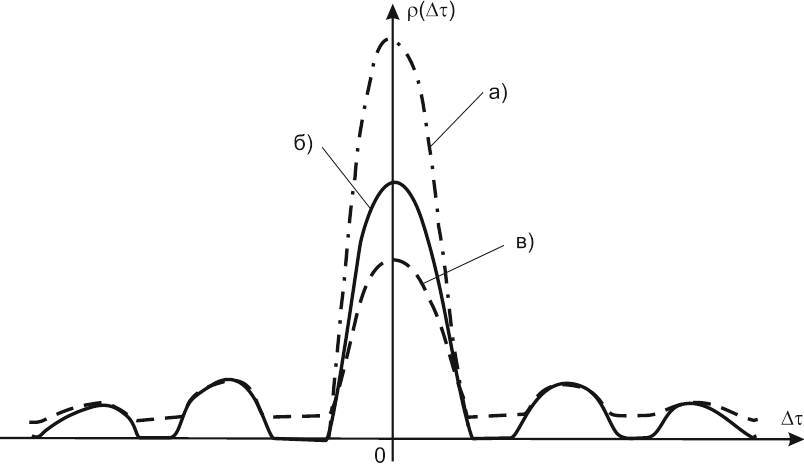
Рис. 4. ПРВ
оценок задержки ![]() при m01>m02>m03: a – m01; б
– m02; в
– m03
при m01>m02>m03: a – m01; б
– m02; в
– m03
Пример искажения исходного сигнала (см. рис. 1) помехами, содержащими флуктуационную и импульсную составляющие, приведен на рис. 5. Кроме того, на рис. 6, а изображен еще один исходный тестовый сигнал, который неоднократно был использован в ходе исследований [3], а на рис. 6, б - этот же сигнал, искаженный негауссовыми помехами. Отметим, что для этих примеров флуктуационная составляющая имеет гауссов закон распределения и дисперсию, постоянную во времени.
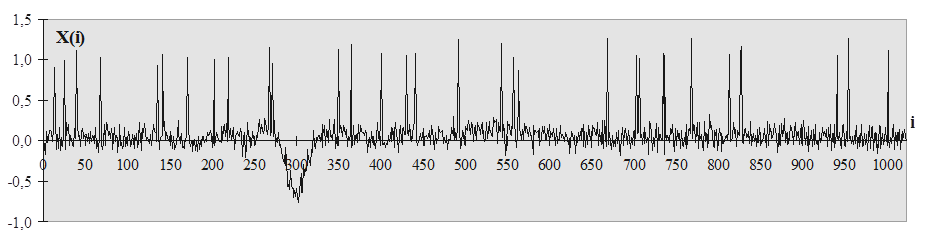
Рис.
5. Временная реализация ЭКГ, искаженной аддитивным шумом с дисперсией 0,003 и
импульсной помехой с ![]() =1,0 и
=1,0 и ![]() =0,03
=0,03
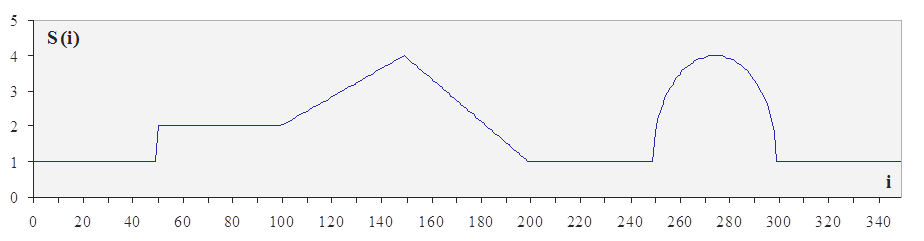
а
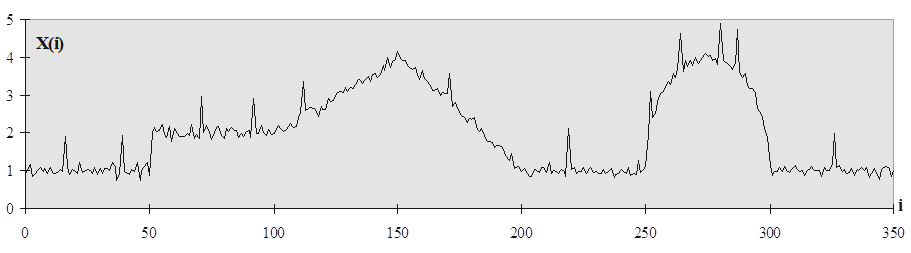
б
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.