Нелинейная фильтрация сигналов: Учебное пособие, страница 12

2)  квазиразмах, вычисляемый как разность между p-й и q-й порядковыми статистиками: , для которых выполняются условия ; на практике наиболее часто используют ; 

3)  минимизированный квазиразмах, рассчитываемый в соответствии с выражением 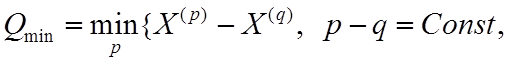 , где ; в отличие от обычного квазиразмаха  менее чувствителен к наличию в выборке значительного числа () односторонних выбросов.

В заключение отметим, что существуют также методы устойчивого оценивания статистик более высоких порядков, в частности коэффициентов асимметрии и эксцесса.

Контрольные вопросы

1. Каковы основные требования к оценкам?

2. Дайте определения несмещенности, состоятельности и эффективности оценок?

3. Какие типы оценок Вы знаете?

4. Что такое устойчивость?

5. Что такое порядковая статистика?

6. Как определяется оценка Вилкоксона?

5. НАИБОЛЕЕ ИЗВЕСТНЫЕ КЛАССЫ НЕЛИНЕЙНЫХ ФИЛЬТРОВ

Нелинейные фильтры можно классифицировать по различным признакам, например:

-  по эффективности подавления помех или сохранения характерных фрагментов сигналов;

-  типам сигналов и помех, для которых применение данной группы фильтров наиболее целесообразно;

-  степени устойчивости к импульсным помехам;

-  типу оценок, положенных в основу алгоритма фильтрации;

-  другим признакам.

В связи с многообразием возможностей классификации ниже приведено краткое описание основных, наиболее часто применяемых типов фильтров, рассмотрены их наиболее интересные и полезные свойства и недостатки, указаны модификации.

Медианный фильтр. Пожалуй, самым известным и давно предложенным как альтернатива линейным фильтрам для случаев воздействия смешанных (гауссовых аддитивных и импульсных) помех является стандартный медианный фильтр (9) [2, 6, 10]. Преимущества стандартного медианного фильтра (СМФ), обусловившие его широкое применение, состоят в следующем. Во-первых, СМФ является одним из лучших нелинейных фильтров в плане устранения импульсных помех, а также подавления помех смешанного вида при достаточно большой вероятности  или негауссовых помех, которые характеризуются ПРВ с большими коэффициентами эксцесса (имеют закон распределения с "тяжелыми хвостами"). Во-вторых, при отсутствии помех СМФ без искажений сохраняет фрагменты сигналов типа «резкий перепад» и «наклонный перепад» (см. рис. 9), а также ряд других фрагментов, например сигнал типа "ломаная" и др. (окрестности отсчетов с  для тестового сигнала на рис. 6, а). Если шум присутствует, то СМФ, как и любые другие нелинейные фильтры, вносит некоторые искажения при обработке таких фрагментов, но уровень этих искажений для СМФ небольшой, и он меньше, чем для большинства других нелинейных фильтров. В-третьих, если СМФ и вносит искажения для характерных фрагментов сигнала, как это, например, имеет место для окрестностей пикообразных и полиномиальных экстремумов ( для тестового сигнала на рис. 6, а), то эти искажения, как правило, невелики по сравнению с искажениями, вносимыми другими фильтрами (см. разд. 7).

Кроме того, для СМФ легко рассчитать длительности импульсов прямоугольной формы  (для сигналов, подобных изображенному на рис. 2, а), при которых они будут сохранены () или устранены (), где  – временная дискретность обрабатываемых данных. Тогда с учетом специфики решаемой задачи легко выбрать размер скользящего окна СМФ -, где  – минимальная длительность прямоугольного импульса, который необходимо сохранить, выраженная числом отсчетов.

Среди недостатков СМФ отметим недостаточно высокую эффективность подавления помех с ПРВ, близкой к гауссовой, как на участках примерно постоянного сигнала, так и особенно на участках быстрого изменения  (например, ,  для сигнала на рис. 6, а). Этот эффект более подробно рассмотрен и проиллюстрирован в разд. 8. Отметим, что зависимость эффективности подавления помех от характера поведения сигнальной составляющей является одним из проявлений нелинейности и отличий нелинейных фильтров от линейных. Выходные сигналы ряда нелинейных фильтров для тестового сигнала, показанного на рис. 8, приведены в Приложении.