Нелинейная фильтрация сигналов: Учебное пособие, страница 10

         Устойчивые  оценки  подразделяют  на  три  класса:   L-,  R-  и M-оценки [7, 12]. Рассмотрим их более подробно.

L-оценки. Ранее уже упоминалось медиана выборки, которая представляет собой центральный элемент упорядоченной выборки

,                          (11)

если N_S – нечетное, и полусумму N_S /2-го и (N_S/2)+1-го элементов, если N_S – четное.

         При этом обозначение X^(j) используется для так называемой j-й порядковой статистики. Таким образом, Х⁽¹⁾ – минимальное значение, а  – максимальное в данной выборке.

         Тогда L-оценка имеет вид [7, 12]

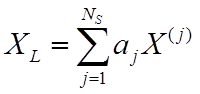                                                ,              (12)

где a_j, j = 1,…,N_S – весовые коэффициенты. В соответствии с такой записью для медианы все коэффициенты  a_j  равны 0, кроме a_(Ns+1)/2=1, если N_S – нечетное, или a_Ns/2 = a_(Ns/2)+1 = 0,5, если N_S – четное. Более того, среднее выборки также является частным случаем L-оценки, для которой все a_j = 1/ N_S.

         Если в выборке имеется выброс, то в упорядоченной выборке вида (11) соответствующий элемент занимает либо первую, либо последнюю позицию, то есть является первой или N_S-й порядковой статистикой. Если же для используемой L-оценки соответствующий весовой коэффициент a_j  равен нулю, то очевидно, что выброс не оказывает влияния на  X_L. Именно за счет выбора равными нулю некоторого количества N_a1 первых весовых коэффициентов a_j, j = 1,…,N_a1 и N_a2 последних весовых коэффициентов a_j, j = n-N_a2+1,…,n обеспечиваются робастные свойства L-оценок, причем чем больше N_a1 и N_a2, тем выше устойчивость, т.е. способность оценки быть слабочувствительной к наличию грубых погрешностей в обрабатываемой выборке. Остальные ненулевые коэффициенты a_j, j = N_a1+1,…,n-N_a2 при этом могут быть выбраны таким образом, чтобы обеспечивать несмещенность L-оценки и минимизировать ее дисперсию.

         Частным случаем L-оценки является a-урезанное среднее

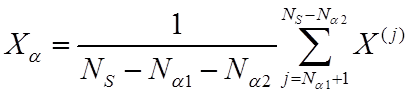                                  ,                                                           (13)

для которой a_j = 1/(n-N_a1-N_a2), j=N_a1+1,…,n-N_a2, а остальные a_j равны 0.

Варьируя N_a1 и N_a2 или соотношения a₁ = N_a1/n и a₂ = N_a2/n, можно изменять характеристики X_a, делая эту оценку более устойчивой при увеличении параметров урезания (усечения). Предельным случаем a-урезанного среднего является медиана выборки при a₁ = a₂®0,5 или определенная порядковая статистика при неравных a₁ и a₂.

         Отметим, что L-оценки полезны не только для обеспечения устойчивости. Для многих распределений при Р_о = 0 к классу L-оценок принадлежат и эффективные, т.е. обеспечивающие минимальную дисперсию, оценки, которые также иногда называют оптимальными. Так, медиана является оптимальной (точнее, квазиоптимальной) оценкой для лапласовского распределения, оценка (+)/2 – для равномерного распределения, а L-оценка, коэффициенты которой a_j медленно возрастают при увеличении j, – для релеевского [14].

         R-оценки. Эти оценки основываются на ранговых критериях. Под рангом понимают номер элемента исходной выборки в полученном для нее вариационном ряду , то есть ранг элемента представляет собой натуральное число от 1 до N_S. Например, если исходная выборка состоит из семи элементов: 11, 5, 2, 8, -13, 4, 6, то упорядоченная выборка (вариационный ряд) будет иметь вид -13, 2, 4, 5, 6, 8, 11. Следовательно, ранги будут: R₁ = 7, R₂ = 4, R₃ = 2, R₄ = 6, R₅ = 1, R₆ = 3, R₇ = 5.      

Одним из примеров R-оценки является оценка Вилкоксона [2]

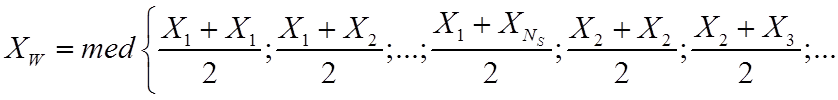
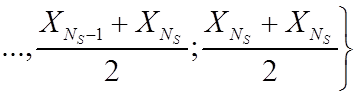
где med{ } означает расчет медианы. Иными словами, X_W есть медиана расширенной выборки размером 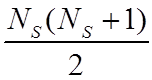,  сформированной из элементов исходной выборки и всех возможных попарных средних.

Оценка Вилкоксона способна ²устранять² до N_B » (0,25…0,3)N_S выбросов одного знака, то есть измерений, существенно  отличающихся от истинного значения параметра либо в меньшую, либо в большую сторону. Вообще, величина e* = N_B/N_S является одной из основных характеристик устойчивости оценки и для медианы при n®¥ e* стремится к 0,5 для X_a при a₁ = a₂  e* = a₁ = a₂ .