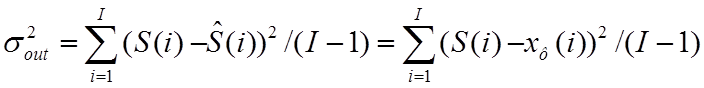Нелинейная фильтрация сигналов: Учебное пособие, страница 5

            (4)

по сравнению с дисперсией шума на его входе 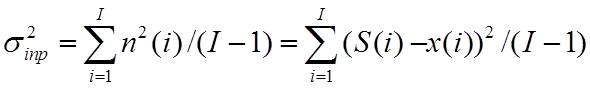 , т.е. 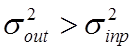. Такое может произойти и тогда, когда применяемый фильтр плохо приспособлен для рассматриваемого класса сигналов и помех. Естественно, что в этом случае применять фильтрацию не имеет смысла.                             

Контрольные вопросы

1. Каковы основные отличия методов линейной и нелинейной фильтрации?

2. В каких практических ситуациях целесообразно применять нелинейные фильтры?

3. Назовите основные типы помех. В чем их отличия?

4. Как определяется среднеквадратическая ошибка на выходе фильтра?

2. ТРЕБОВАНИЯ К МЕТОДАМ НЕЛИНЕЙНОЙ ФИЛЬТРАЦИИ.

КРИТЕРИИ ЭФФЕКТИВНОСТИ

      Основные требования к методам нелинейной фильтрации одномерных сигналов (процессов) несколько отличаются от требований к линейным фильтрам, но общими требованиями для них являются:

-  эффективное подавление флуктуационных помех;

-  внесение в результате фильтрации минимальных искажений;

-  обеспечение приемлемого быстродействия.

Вместе с тем в требование минимизации вносимых искажений для нелинейных фильтров вкладывается несколько иной смысл. Прежде всего подразумевается, что необходимо обеспечить минимальные искажения для окрестностей характерных точек сигнальной составляющей – фрагментов, содержащих перепады, пики, локальные экстремумы и т.д. В частности, для тестового сигнала, показанного на рис. 6, а, такими фрагментами являются окрестности отсчетов с индексами 50, 100, 150, 200, 250 и 300.        

         Кроме того, специфическим и часто первостепенным требованием к методам нелинейной фильтрации является надежное устранение импульсных помех (выбросов) или, в более общем плане, способность обеспечивать приемлемое функционирование в условиях воздействия негауссовых помех при ограниченной априорной информации об их статистических характеристиках. 

Таким образом, к нелинейным фильтрам предъявляется ряд противоречивых требований. В частности, как будет показано в разд. 7 и 8, для нелинейных неадаптивных фильтров сложно достичь высокой эффективности подавления флуктуационных помех при минимальных вносимых искажениях и достаточной устойчивости к импульсным помехам. Кроме того, для конкретных приложений приоритет, то есть степень важности, перечисленных выше требований может быть различным. Именно поэтому на данный момент разработаны и предложены сотни различных нелинейных фильтров, и выбор наилучшего из них или разработка нового фильтра применительно к конкретной ситуации являются в значительной степени эмпирическими, поскольку в литературе отсутствуют четкие рекомендации и во многих случаях "хорошие" решения находят на основе имеющихся у разработчика опыта и эрудиции.

         Естественно, что характеристики нелинейных фильтров хотелось бы описать аналитически и представить количественно хотя бы для того, чтобы иметь возможность сравнивать между собой различные методы фильтрации и делать обоснованный выбор в пользу того или иного алгоритма. Такая возможность существует не всегда вследствие причин, которые будут обсуждены позднее. Однако  существует и достаточно широко используется ряд общепринятых критериев (количественных показателей) эффективности нелинейных фильтров.

         Эти критерии можно отнести к трем категориям:  интегральные, локальные, специальные.

         Интегральные количественные показатели. По аналогии с методами линейной фильтрации для нелинейных фильтров широко используются среднеквадратическая ошибка (4) и среднемодульное отклонение (СМО)

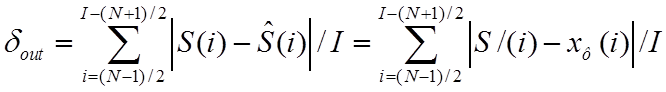         .                                                           (5)

Примечание.  Суммирование в (5) проводят не от 1 до I, а от  до  (где N – размер скользящего окна фильтра) для того, чтобы устранить влияние так называемых краевых эффектов на  или .