Нелинейная фильтрация сигналов: Учебное пособие, страница 7

Стабильной точкой нелинейного фильтра называют такой входной сигнал, который при прохождении через фильтр не изменяется, то есть  [2]. Возможно, более точно отражает суть используемый в англоязычной литературе термин «root signal»,  т.е. «корневой сигнал». Одними из стабильных точек обычного медианного фильтра являются сигналы ²резкий перепад² ("step edge") и ²наклонный перепад² ("ramp edge"), которые показаны на рис. 9.

а	б

Рис. 9. Сигналы ²резкий перепад² (а) и ²наклонный перепад² (б)

Контрольные вопросы

1. Каковы основные требования к нелинейным фильтрам?

2. Какие критерии качества (эффективности) фильтрации Вы знаете?

3. В чем отличие интегральных и локальных показателей? Почему следует анализировать и те, и другие?

4. Что такое «стабильная точка» нелинейного фильтра?

3. ПРИНЦИП ФИЛЬТРАЦИИ В СКОЛЬЗЯЩЕМ ОКНЕ

Большинство методов нелинейной фильтрации предусматривают обработку данных в скользящем окне, что аналогично принципу действия линейных фильтров с конечной импульсной характеристикой (КИХ). Фильтрация в скользящем окне подразумевает, что некоторому (одному) i-му отсчету, обычно центральному, присваивается выходное значение в результате применения некоторого метода обработки к выборке данных, состоящей из значений N-1 отсчетов, соседних с i-м, и значения для самого i-го отсчета. Самым простым примером такой обработки может быть линейный усредняющий фильтр (ЛУФ), для которого

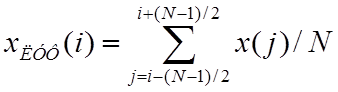  .                                      (8)

Согласно выражению (8) при формировании выходного значения  учитываются значения исходного процесса для отсчетов с индексами от  до, которые входят в скользящее окно с центром в i-м отсчете. Простейшим примером нелинейной обработки данных в скользящем окне является расчет медианы, лежащей в основе стандартного медианного фильтра

.             (9)

Напомним, что расчет медианы выборки (см. также разд. 5) предусматривает сортировку выборки данных в порядке возрастания и выбор среднего (по положению в отсортированной выборке) значения. Например, если размер выборки данных N_s=7 и исходная выборка включает в себя значения 2, 5, 3, 3, 4, 5, 10, то отсортированная выборка (вариационный ряд) имеет вид 2, 3, 3, 4, 5, 5, 10 и, соответственно, медиана равна 4.    

В большинстве случаев выходное значение фильтра присваивается центральному отсчету скользящего окна (в противном случае для получения  учитываются отсчеты с индексами от  до, где  и). В связи с этим размеры скользящих окон, характеризуемые количеством входящих в них отсчетов, обычно являются нечетными – 3, 5, 7 и т.д. На практике нечасто используют.          

Принцип нелинейной фильтрации в скользящем окне имеет определенное логическое обоснование. Поскольку нелинейные фильтры, в основном, применяются для обработки сигналов и процессов, содержащих фрагменты с резким изменением сигнальной (информационной) составляющей , то значения, отстоящие от  достаточно далеко, редко имеют высокую степень корреляции с значениями . Следовательно, для получения 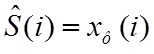 нецелесообразно учитывать, для которых  достаточно велико. Кроме того, при небольших, как правило, легче обеспечить более высокое быстродействие алгоритма фильтрации, чем при обработке данных в скользящих окнах большого размера или с учетом всех отсчетов, предшествовавших i-му.

При алгоритмической реализации и исследовании свойств методов нелинейной фильтрации в скользящем окне приходится сталкиваться с небольшой практической проблемой (краевой задачей): как осуществлять обработку  первых и последних отсчетов? Например, для  в начале обрабатываемого сигнала для расчета  получается, что необходимо иметь, которых просто нет. В этом случае обычно используют один из трех возможных способов:

1)  при  в начале сигнала и  в конце сигнал вообще не обрабатывают, то есть  присваивают исходные значения;

2)  при  или  применяют тот же тип фильтра, что и для всей остальной части сигнала, но с таким (разным для разных ), чтобы выполнялись соответственно равенства  и ; первому и последнему отсчетам  присваивают исходные значения;