Фильтры на основе порядковых статистик. В принципе, L-фильтры и АУФ могут быть отнесены к этому широкому классу фильтров. Однако многие фильтры на основе порядковых статистик (ФПС) не относятся к L-фильтрам. В частности, это справедливо для взвешенных ФПС (ВФПС - weighted order statistic filter), для которых
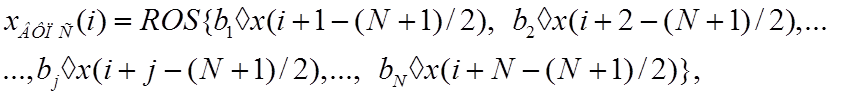 (16)
(16)
где ROSозначает
операцию расчета R-йпорядковой статистики выборки данных, ![]() –
набор коэффициентов дуплицирования (целых неотрицательных чисел), знак
–
набор коэффициентов дуплицирования (целых неотрицательных чисел), знак ![]() определяет операцию дуплицирования
(размножения), то есть включения в формируемую расширенную выборку
определяет операцию дуплицирования
(размножения), то есть включения в формируемую расширенную выборку ![]() раз значения отсчета
раз значения отсчета ![]() .
.
Очевидно,
что в отличие от L-фильтров ВФПС аналогично
линейным фильтрам учитывает положение данного элемента относительно
центрального элемента скользящего окна путем присвоения ему соответствующего ![]() при формировании расширенной выборки из исходной.
Путем варьирования
при формировании расширенной выборки из исходной.
Путем варьирования ![]() возможно изменение в широких
пределах основных свойств ВФПС.
возможно изменение в широких
пределах основных свойств ВФПС.
Однако
в связи с многообразием возможных вариантов – бесконечным числом возможных
сочетаний целочисленных коэффициентов дуплицирования – анализ свойств ВФПС
сложен и практическое применение находят лишь простейшие из них, например
центрально-взвешенный медианный фильтр (ЦВМФ). Для этого фильтра в выражении
(16) все ![]() , кроме
, кроме ![]() , равны
1,
, равны
1, ![]() выбирается равным положительному нечетному
числу (3, 5, 7 и т.д.), а
выбирается равным положительному нечетному
числу (3, 5, 7 и т.д.), а ![]() для того, чтобы R-япорядковая статистика совпадала с медианой расширенной выборки, которая для
ЦВМФ содержит
для того, чтобы R-япорядковая статистика совпадала с медианой расширенной выборки, которая для
ЦВМФ содержит ![]() элементов. При небольших отношениях
элементов. При небольших отношениях
![]() свойства ЦВМФ и СМФ весьма близки. Однако
ЦВМФ чуть лучше сохраняет характерные фрагменты, но хуже подавляет помехи. При
свойства ЦВМФ и СМФ весьма близки. Однако
ЦВМФ чуть лучше сохраняет характерные фрагменты, но хуже подавляет помехи. При ![]() ЦВМФ вырождается в идемпотентный (idempotent)
фильтр, то есть фильтр, для которого
ЦВМФ вырождается в идемпотентный (idempotent)
фильтр, то есть фильтр, для которого ![]() для любых входных
сигналов.
для любых входных
сигналов.
Приведем
пример расчета выходного значения ЦВМФ с N=
5 и ![]() . Предположим, что исходная
последовательность значений отсчетов имеет вид 2, 5, 5, 3, 6, 4, 7 и т.д. Рассчитаем
. Предположим, что исходная
последовательность значений отсчетов имеет вид 2, 5, 5, 3, 6, 4, 7 и т.д. Рассчитаем
![]() , для которого при N=
5 в скользящее окно входят элементы 5, 5, 3, 6, 4, а расширенная выборка при
, для которого при N=
5 в скользящее окно входят элементы 5, 5, 3, 6, 4, а расширенная выборка при ![]() имеет вид 5, 5, 3, 3, 3, 6, 4. Тогда
отсортированная выборка будет 3, 3, 3, 4, 5, 5, 6 и R-япорядковая статистика (напомним, что
имеет вид 5, 5, 3, 3, 3, 6, 4. Тогда
отсортированная выборка будет 3, 3, 3, 4, 5, 5, 6 и R-япорядковая статистика (напомним, что![]() ) равна
4, то есть
) равна
4, то есть ![]() = 4.
= 4.
Фильтры
на основе М- и R-оценок.
Упомянутые
выше М- и R- оценки (см. разд. 4) также
могут использоваться при нелинейной фильтрации в скользящем окне, т.е.
выходному значению ![]() присваивается результат
применения соответствующего алгоритма оценивания к выборке входных значений для
присваивается результат
применения соответствующего алгоритма оценивания к выборке входных значений для
![]() . Так функционирует фильтр Вилкоксона (ФВ):
. Так функционирует фильтр Вилкоксона (ФВ):
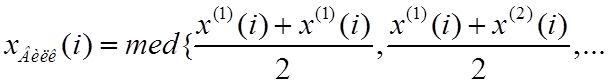
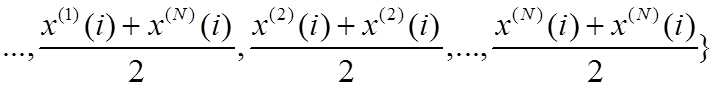 .
.
Таким
образом, для фильтра Вилкоксона, как и для ВФПС, формируется расширенная
выборка, размер который равен ![]() . ФВ является одним из
лучших фильтров в плане эффективности подавления смешанных помех, однако его
способность сохранять характерные фрагменты сигнальной составляющей весьма
низкая. Невысоким (в сравнении со многими другими ФПС) является и быстродействие
ФВ, поскольку даже при небольших размерах скользящего окна приходится
осуществлять сортировку (представление значений в упорядоченном виде) выборки
значений значительного размера, что ограничивает практическое применение ФВ.
. ФВ является одним из
лучших фильтров в плане эффективности подавления смешанных помех, однако его
способность сохранять характерные фрагменты сигнальной составляющей весьма
низкая. Невысоким (в сравнении со многими другими ФПС) является и быстродействие
ФВ, поскольку даже при небольших размерах скользящего окна приходится
осуществлять сортировку (представление значений в упорядоченном виде) выборки
значений значительного размера, что ограничивает практическое применение ФВ.
Выходное значение мириадного фильтра определяется в виде
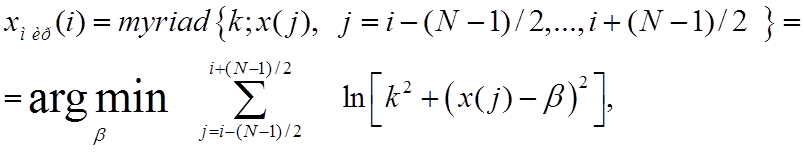 (17)
(17)
где k –
настроечный параметр, myriad
означает операцию определения мириады выборки, 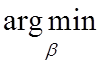 –
координата глобального минимума функции по заданному параметру b.
Быстродействие этого фильтра также невелико, так как для каждого положения
скользящего окна приходится решать задачу поиска наименьшего минимума функции
–
координата глобального минимума функции по заданному параметру b.
Быстродействие этого фильтра также невелико, так как для каждого положения
скользящего окна приходится решать задачу поиска наименьшего минимума функции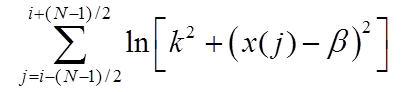 .
.
Отметим,
что мириадный фильтр обладает высокой нелинейностью и своеобразием
статистических и динамических характеристик, которые существенно зависят от
параметра k. При ![]() , где
, где ![]() – СКО
флуктуационных помех, мириадный фильтр обладает способностью подавлять
смешанные помехи и сохранять резкий перепад не хуже, чем СМФ. При
– СКО
флуктуационных помех, мириадный фильтр обладает способностью подавлять
смешанные помехи и сохранять резкий перепад не хуже, чем СМФ. При ![]() свойства мириадного фильтра близки к
свойствам ЛУФ. Следовательно, для обеспечения необходимого компромисса свойств
мириадного фильтра необходимо либо априорно знать, либо оценивать
статистические характеристики помех. Это отличает мириадный фильтр от всех
ранее рассмотренных нелинейных фильтров, для которых при работе соответствующих
алгоритмов такая информация не используется. Впрочем, наличие такой информации
полезно и желательно при выборе нелинейного фильтра для решения конкретной
задачи.
свойства мириадного фильтра близки к
свойствам ЛУФ. Следовательно, для обеспечения необходимого компромисса свойств
мириадного фильтра необходимо либо априорно знать, либо оценивать
статистические характеристики помех. Это отличает мириадный фильтр от всех
ранее рассмотренных нелинейных фильтров, для которых при работе соответствующих
алгоритмов такая информация не используется. Впрочем, наличие такой информации
полезно и желательно при выборе нелинейного фильтра для решения конкретной
задачи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.