Нелинейная фильтрация сигналов: Учебное пособие, страница 16

         Особое место занимают методы гомоморфной фильтрации, включающие в себя фильтр геометрического среднего [2, 3]. Гомоморфным преобразованием называется такое преобразование , для которого при  выполняется условие . Таким преобразованием, в частности, является логарифмическое, если . При применении преобразования типа  к сигналу , , описываемому моделью (3), получаем

         ,                                                          (21)

т.е. мультипликативная помеха становится аддитивной по отношению к сигнальной составляющей . Поскольку случай воздействия аддитивных помех более прост и хорошо изучен, то во многих практических ситуациях выполнение  вида (20) способствует более эффективной фильтрации или упрощает выбор алгоритма обработки данных. Более того, если МО m равно 1 и 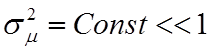, то имеем

                                  , (22)

где МО  примерно равно нулю, а дисперсия примерно равна .

         Эмпирические и другие нелинейные фильтры. Кроме рассмотренных выше классов методов нелинейной фильтрации, существует и множество других. В частности, это морфологические, полиномиальные, основанные на принятии решений, подчеркивающие перепады и устраняющие импульсы, стековые, итеративные, каскадные, рекурсивные [2] и т.д. В основе некоторых из них лежат теоретические положения (математическая морфология, дискретные ряды Вольтерра, булевы функции, теория пороговой декомпозиции и т.д.), но многие опираются на логические или интуитивные идеи. В частности, это относится к сигнально-зависимым (data-dependent) фильтрам, которые иногда также называют адаптивными, но в несколько ином понимании ²адаптации², чем для традиционных адаптивных фильтров [16].

         Примером может служить сигма-фильтр, для которого для заданного положения скользящего окна при условии известной и неизменной дисперсии аддитивного гауссова шума  выполняют следующие операции:

а) формируют as-окрестность  , где параметр  обычно выбирают равным 2;

б) проверяют значения 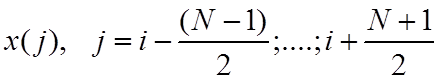 на принадлежность данной окрестности:

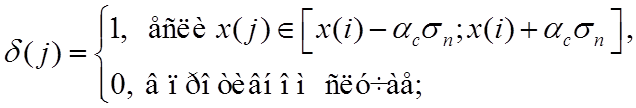             ;                                                          (23)

         в) получают выходное значение сигма-фильтра в виде

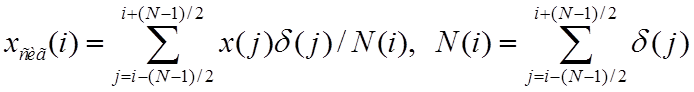      .                                                          (24)

         Таким образом, усреднение проводится только для тех значений в скользящем окне, которые близки к значению центрального отсчета. Благодаря этому хорошо сохраняются перепады и другие особые точки сигнала. Недостатком является неспособность стандартного сигма- фильтра устранять импульсные помехи, но существуют модификации [17], для которых этот недостаток устранен. Кроме того, предполагаются гауссовость и стационарность помех, а также наличие априорной информации о .

         Приведенные классификация и краткий анализ ни в коем случае не претендуют на полноту. Их цель – показать, сколь разнообразны методы нелинейной фильтрации и широки их возможности.       

Контрольные вопросы

1. Каким образом и по каким признакам можно классифицировать нелинейные фильтры?

2. В чем состоит принцип работы a-урезанного фильтра?

3. Как работает сигма-фильтр и какие сведения о помехах необходимы для его функционирования?

4. В чем состоят недостатки фильтра Вилкоксона?

5.  Что такое гомоморфное преобразование?

6. МЕТОДЫ АНАЛИЗА ВЫХОДНЫХ СИГНАЛОВ НЕЛИНЕЙНЫХ ФИЛЬТРОВ

В связи с отмеченными ранее сложностями анализа характеристик нелинейных фильтров, не позволяющими использовать подходы и классификационные критерии, принятые в теории линейной фильтрации, при исследовании выходных сигналов для методов нелинейной фильтрации обычно применяют несколько иные методы. Кратко рассмотрим основные из них.

Для частных ситуаций – заданных характеристик помех, выбранного простого тестового сигнала и рассматриваемого нелинейного фильтра – можно использовать методы теории вероятностей и разработанные методы определения статистических характеристик порядковых статистик (см. определение порядковых статистик выборки данных в разд. 4). Для независимых значений выборки данных с функцией распределения F(x), ПРВ r(x) и размерностью N, что соответствует выборке значений сигнала постоянного уровня при воздействии некоррелированных помех в скользящем окне, функция распределения  и ПРВ  j-й порядковой статистики имеют вид