Однако
![]() и
и ![]() не
способны достаточно адекватно охарактеризовать свойства фильтров. Например,
предположим, что фильтр F1 лучше фильтра F2
подавляет флуктуационные помехи, а фильтр F2 лучше, чем F1,
сохраняет сигнал в окрестностях характерных точек. При этом
не
способны достаточно адекватно охарактеризовать свойства фильтров. Например,
предположим, что фильтр F1 лучше фильтра F2
подавляет флуктуационные помехи, а фильтр F2 лучше, чем F1,
сохраняет сигнал в окрестностях характерных точек. При этом ![]() и
и ![]() для
обоих фильтров могут иметь примерно одинаковые значения и, соответственно,
сделать однозначный вывод о предпочтительности F1 или F2,
сравнивая между собой
для
обоих фильтров могут иметь примерно одинаковые значения и, соответственно,
сделать однозначный вывод о предпочтительности F1 или F2,
сравнивая между собой 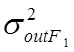 и
и 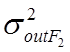 (или
(или ![]() и
и ![]() ),
сложно. Тем не менее если выбор делается из большой группы фильтров F1,
F2, ….., Fn, то, как правило, для наилучшего фильтра
),
сложно. Тем не менее если выбор делается из большой группы фильтров F1,
F2, ….., Fn, то, как правило, для наилучшего фильтра 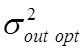 и
и ![]() близки
к
близки
к 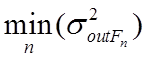 и
и 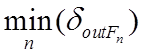 .
.
Локальные количественные показатели. Использование локальных показателей эффективности фильтрации в какой-то мере позволяет устранить неоднозначность трактовки интегральных критериев. При этом появляется возможность более полно изучить характеристики нелинейных фильтров для типичных фрагментов сигналов. Применяют фактически те же количественные показатели, что и в (4) или (5), но рассчитанные локально:
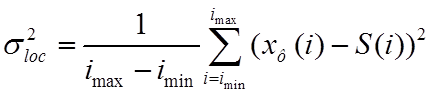 ; (6)
; (6)
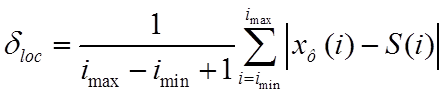 , (7)
, (7)
где
индексы ![]() и
и ![]() определяют
соответственно индексы начала и конца участка, включающего характерную точку
сигнала с индексом
определяют
соответственно индексы начала и конца участка, включающего характерную точку
сигнала с индексом![]() . При этом обычно пользуются
следующим правилом выбора этих индексов:
. При этом обычно пользуются
следующим правилом выбора этих индексов:![]() ;
;![]() . Например, для тестового сигнала,
представленного на рис. 6, а, локальные показатели можно рассчитывать для
участков с
. Например, для тестового сигнала,
представленного на рис. 6, а, локальные показатели можно рассчитывать для
участков с ![]() ,
, ![]() (характеризуют
степень сохранения перепада или единичного скачка);
(характеризуют
степень сохранения перепада или единичного скачка); ![]() ,
, ![]() (степень сохранения пикообразного
экстремума);
(степень сохранения пикообразного
экстремума); ![]() ,
, ![]() (степень
сохранения экстремума, описываемого полиномом второй степени).
(степень
сохранения экстремума, описываемого полиномом второй степени).
Можно
также рассчитывать ![]() или
или ![]() для
участка с
для
участка с ![]() ,
, ![]() , чтобы
определить степени подавления помех для сигнала постоянного уровня, или для
участка с
, чтобы
определить степени подавления помех для сигнала постоянного уровня, или для
участка с ![]() ,
, ![]() , чтобы
охарактеризовать степень подавления помех на линейно изменяющихся участках.
, чтобы
охарактеризовать степень подавления помех на линейно изменяющихся участках.
Анализ локальных критериев позволяет более полно охарактеризовать частные свойства фильтров и способствует более обоснованному выбору наилучшего из них, если четко сформулирован приоритет требований и заранее известно, что сигнал, который предполагается обрабатывать, будет содержать те же типы характерных фрагментов, для которых по тестовому сигналу рассчитывались локальные критерии. Более того, необходимо, чтобы и статистические характеристики помех, при воздействии которых на сигнал рассчитывались количественные показатели, были близки к тем, которые будут иметь место в ситуации, для которой осуществляется выбор или разработка нелинейного фильтра. К сожалению, на практике такой объем априорных сведений о характеристиках сигнала и помех для разработчика часто недоступен.
Специальные количественные показатели. Необходимость использования таких показателей обусловлена рядом факторов, в частности:
а) применением нелинейных фильтров для обработки сигналов (процессов), искаженных импульсными помехами;
б) возможностью предварительного применения фильтрации в целях последующего определения параметров сигнала, используя не исходный процесс x(t), а хф(t).
В первом случае важное значение имеет параметр e*, который характеризует способность фильтра быть мало чувствительным к импульсным помехам (см. далее разд. 4). Этот параметр рассчитывается как отношение Nrem/Ns, где Nrem – число импульсных помех (аномальных измерений) в выборке данных размера Ns, которые могут быть «устранены» благодаря использованию устойчивых (робастных) оценок.
Во втором случае на первый план выходят количественные показатели, характеризующие надежность и точность решения конечной задачи, например, вероятность правильного обнаружения экстремума заданного вида, дисперсия оценок координат характерных точек сигнала – «скачка», пика, перехода через заданный уровень и т.д.
Еще одной специальной характеристикой (но не показателем) некоторых нелинейных фильтров является набор соответствующих им стабильных точек.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.