Нелинейная фильтрация сигналов: Учебное пособие, страница 15

В конце 90-х годов Г. Арсе предложил взвешенный мириадный фильтр, для которого

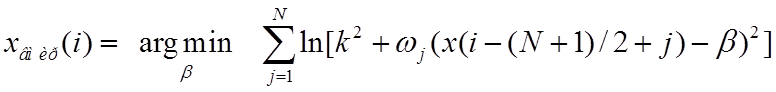,   (18)

где  – весовые коэффициенты. Благодаря этому учитываются положения элементов в скользящем окне и появляется возможность реализовывать функции, аналогичные линейным ФНЧ, ФВЧ и другим, при сохранении робастных свойств.

Как и для обычного мириадного, для взвешенного мириадного фильтра операция поиска глобального минимума функций достаточно трудоемкая, что несколько ограничивает их применение. Поиск облегчается, если учесть тот факт, что глобальный минимум лежит в пределах от минимального до максимального значения данных в обрабатываемой выборке.

Многоэтапные и гибридные медианные фильтры. Для этих фильтров характерно стремление их разработчиков решить одну или несколько задач из следующего перечня:

-  использовать преимущества медианной оценки при фильтрации данных;

-  обеспечить более высокое быстродействие за счет применения медианной или других простых операций к частям (подмножествам) данных, входящих в выборку, с последующим объединением их результатов (это более типично для решения задач обработки изображений, а не одномерных сигналов);

-  учесть порядок (временной или пространственный) расположения отсчетов в исходной выборке, формируемой для текущего положения скользящего окна.

Методику достижения перечисленных целей проще всего проиллюстрировать на конкретном примере. Для КИХ-гибридного медианного фильтра (КГМФ) выходное значение получают в виде 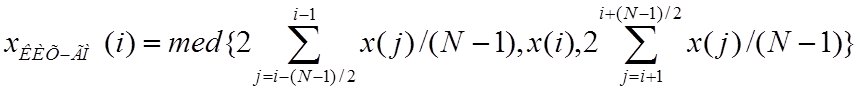   , (19)

то есть находят медианное значение для выборки, содержащей всего три значения, два из которых получены как средние по так называемым субапертурам, включающим соответственно все элементы "слева" от центрального отсчета скользящего окна () и все отсчеты "справа" от него ().

Таким образом, для КГМФ обычно удается достичь высокого быстродействия благодаря использованию простейших операций с выборками данных малой размерности и их конвейерному (последовательному) выполнению. Кроме того, удается учесть расположение отсчетов в скользящем окне вследствие использования субапертур, обеспечить способность сохранять фрагменты типа «резкий перепад» и «наклонный перепад», а также некоторую устойчивость к импульсным помехам благодаря медианной операции.

Существует достаточно большое количество разновидностей многоэтапных и гибридных медианных фильтров, отличающихся между собой числом значений, для которых на конечном шаге рассчитывается медиана, методиками получения выходных значений субапертур (например, может использоваться линейная экстраполяция) и т.д. Их общими преимуществами являются отсутствие или малый уровень динамических ошибок, сравнительная простота и высокое быстродействие.

Приведем пример работы простейшего КИХ-медианного гибридного фильтра с N= 5. Снова предположим, что исходная последовательность значений отсчетов имеет вид 2, 5, 5, 3, 6, 4, 7 и т.д. Рассчитаем, для которого при N= 5 в скользящее окно входят элементы 5, 5, 3, 6, 4. Соответственно в первую субапертуру попадают значения 5 и 5, а во вторую - 6 и 4. Выходное значение для первой субапертуры равно (5+5)/2=5, для второй – (6+4)/2=5. Медианное значение для выходов субапертур и значения центрального отсчета (5, 5, и 3) равно 5, то есть  = 5. 

         Нелинейные усредняющие и гомоморфные фильтры. Нелинейные усредняющие фильтры (НУФ) в обобщенном виде описываются выражением

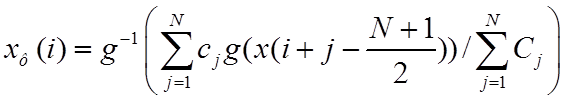                      ,                                                           (20)

где– функция, имеющая обратную функцию , c_j, j = 1,….,N – весовые коэффициенты. Кроме того, после выполнения преобразования  вместо взвешенного усреднения (20) могут использоваться и другие операции с полученной выборкой  данных, включая нелинейные. Наиболее часто используют функции вида  (гармонический усредняющий фильтр),  (фильтр геометрического среднего), 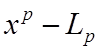 (усредняющий фильтр). Эти фильтры способны подчеркивать или нивелировать те или иные типы деталей в обрабатываемых сигналах. Очевидно, что при этом сигнал должен быть положительно определенным.