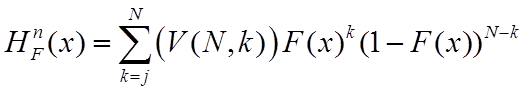Нелинейная фильтрация сигналов: Учебное пособие, страница 17

,                      (25)

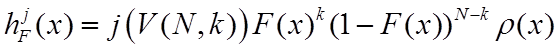,                    (26)

где V(N,k) – число сочетаний из N по k. Совместное распределение порядковых статистик с номерами j и l (j<l) описывается выражением

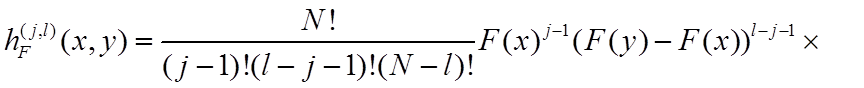
.                               (27)

         На основе (25) и (26) могут быть вычислены математические ожидания, дисперсии и моменты более высоких порядковых для порядковых статистик. Для L-фильтра очевидно, что МО 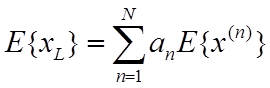 (Е обозначает усреднение), а дисперсия 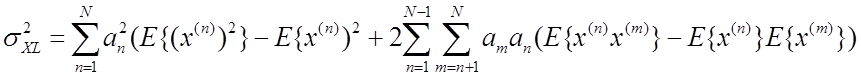. (28)

К сожалению, в большинстве случаев аналитический расчет основных статистических характеристик порядковых статистик затруднен, в связи с чем применяются методы численного интегрирования.

Однако и методы численного интегрирования не всегда дают достаточно точные результаты, особенно если ПРВ r(x) имеет "тяжелые хвосты". Кроме того, формулы (25) и (26) применимы только в том случае, если r(x) – непрерывная функция аргумента. В противном случае, например, для распределения (2), справедливы выражения, отличные от (25) и (26).

В связи с отмеченными сложностями строгие математические методы анализа статистических характеристик  выходных сигналов нелинейных фильтров удается применить не всегда. Аналитические расчеты оказываются успешными, то есть приводят к получению выражений в явном виде, при выполнении следующих условий:

-  сигнал задан аналитически в виде простых функций, например, участка прямой (сигнал постоянного уровня или изменяющийся линейно), резкого перепада, синусоиды и т.д.;

-  помехи описываются достаточно простыми законами распределения (гауссовый, лапласовский, релеевский шум), они не коррелированны и сигнально-независимы;

-  рассматриваемый фильтр достаточно прост, например, основывается на использовании небольшого числа порядковых статистик.

Приведем некоторые результаты для одного из простейших случаев – сигнала постоянного уровня, искаженного аддитивным шумом с МО, равным нулю. Рассмотрим стандартный медианный фильтр с большим размером скользящего окна (N> 100). Эффективность подавления помех при использовании СМФ сравним с эффективностью подавления помех ЛУФ с тем же N, для чего приведем соотношение дисперсий остаточных флуктуаций  (исходное значение дисперсии помех  при этом роли не играет, расчеты могут быть проведены аналитически [2, 3]). Это соотношение зависит от ПРВ помех: для гауссовых помех , для лапласовской ПРВ  и для равномерно распределенного шума . Таким образом, в зависимости от ПРВ помех СМФ может подавлять шум как более, так и менее эффективно, чем ЛУФ. Для гауссовой ПРВ помех известно аналитическое выражение для определения  при различных N:                       

,                          (29)

т.е. при увеличении Nэффективность подавления помех, характеризуемая соотношением , возрастает примерно пропорционально N. Такая зависимость, типичная для линейных фильтров, имеет место и для многих нелинейных фильтров (например, ФВ и АУФ), но не для всех. Например, для сигма-фильтра эффективность подавления помех растет медленнее, чем прямо пропорционально N.

Вместе с тем приведенный ниже пример показывает, что увеличение размера скользящего окна при обработке даже сравнительно простых сигналов не всегда приводит к положительному эффекту в плане уменьшения среднеквадратической ошибки  (4) на выходе фильтра. Рассмотрим процесс, для которого сигнальная составляющая имеет  вид не содержащей разрывы функции S(t_i) = arctg(y_art_i), где  y_ar=1, , , Dt = 0,016, которая хорошо описывает, например, изменение угловых координат объекта при его прямолинейном равномерном движении. Эффективность нелинейной фильтрации оценим, используя среднеквадратическую ошибку , которую получим путем усреднения для достаточно большого числа реализаций значений c, рассчитываемых для каждой реализации:

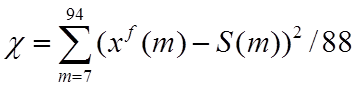                           .                             (30)