Нелинейная фильтрация сигналов: Учебное пособие, страница 13

Здесь же уместно проиллюстрировать невыполнение для СМФ первого условия линейности, указанного в разд. 1. Рассмотрим окрестность характерного фрагмента – точки перепада в предположении, что сигнал искажен гауссовым шумом с математическим ожиданием, равным 0, и дисперсией порядка 2,0. Поскольку речь идет о цифровой обработке, то предполагается, что значения  – целые числа. Для данного примера.

В табл. 1 приведены значения , , , и , , а также ,  (результат применения СМФ к сигнальной составляющей и шуму раздельно) и  для .

Таблица 1

Иллюстрация свойств СМФ

Таким образом,  для i= 4, 5 и 6, то есть условие линейности не выполняется. Более того, вследствие влияния помех  для  перепад оказывается ²сглаженным².

         В связи с тем, что СМФ, основанный на использовании устойчивой оценки и одновременно (N+1)/2-й порядковой статистики, характеризуется перечисленными выше преимуществами, в 80-е годы прошлого столетия основное внимание в области нелинейной фильтрации уделялось разработке и анализу свойств фильтров, в основу которых также положены порядковые статистики и методы робастного оценивания (см. разд. 4). Количество таких фильтров велико, и, обсуждая проблему выбора, авторы монографии “Fundamentals of Nonlinear Filtering” [2] Я. Астола и П. Куосманен говорят: ²Тысяча задач – тысяча решений². Поэтому ниже приведем основные группы фильтров данного класса и некоторых их представителей.

L-фильтры. Для этого широкого класса нелинейных фильтров, к которому можно отнести и СМФ, выходное значение получают в виде

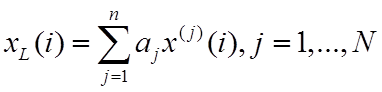         ,                                  (14)

где  – j-я порядковая статистика для выборки данных, сформированной из значений элементов, принадлежащих скользящему окну размером N, центр которого расположен в i-м элементе фильтруемого процесса, – j-й весовой коэффициент.

Так же, как и свойства L-оценок можно в широких пределах изменять путем варьирования или выбора соответствующих наборов весовых коэффициентов , свойства L-фильтров можно изменять, достигая того или иного компромисса между устойчивостью к импульсным помехам, сохранением характерных фрагментов и подавлением флуктуационных помех. Более того, по аналогии с линейными адаптивными фильтрам на основе L-фильтров разработаны методы и алгоритмы нелинейной адаптивной фильтрации, для которых адаптация осуществляется путем подстройки .

Частным   случаем   L-фильтра   является   фильтр   на  основе a-урезанного среднего (trimmed mean), который также часто называют просто a-урезанным фильтром (АУФ)

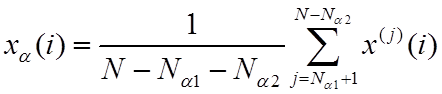                                 ,                                                           (15)

где N_a1и N_a2 – количество отбрасываемых в отсортированной выборке минимальных и максимальных значений соответственно.

Обычно на практике используют равные друг другу значения N_a1 и N_a2 или соотношения a₁=N_a1/N=a₂=N_a2/N. Свойства АУФ можно варьировать за счет изменения a. При больших a (порядка 0,4) они близки к свойствам СМФ, при малых a (порядка 0,1) – к свойствами ЛУФ при тех же N.