Цифровые устройства и микропроцессоры: Учебное пособие, страница 8

                                    X+X+X+X = X

                                    X*X*X*X = X

б) переместительности

                            A+B+C+D = A+C+B+D

в) сочетательности

                                 A+B+C+D = A+(B+C)+D = A+B+(C+D)

г) распределительности

               X₁ (X₂+X₃) = X₁X₂ + X₁X₃

                       X₁+X₂X₃= (X₁+X₂ ) (X₁+X₃ ) = / докажем это путём раскрытия скобок / =

                   = X₁X₁+ X₁X₃+ X₁X₂+ X₂X₃ = X₁ (1+X₃+X₂) + X₂X₃ = X₁+X₂X₃

4. Правило поглощения (одна переменная поглощает другие)

                             X₁+X₁X₂ X₃ = X₁ (1+X₂ X₃  ) = X₁

5. Правило склеивания  (выполняется только по одной переменной)

                           

Также как в обычной математике имеется старшинство операций:

        1)  Действие в скобках

        2)  Операция с одним операндом (одноместная операция) –НЕ

        3)  Конъюнкция   - И

        4)  Дизъюнкция   - ИЛИ 

        5)  Сумма по модулю два.

Операции одного ранга выполняются слева направо в порядке написания.

Алгебра логики линейна и для неё справедлив принцип суперпозиции.

Используя законы алгебры логики, можно преобразовывать ФАЛ и переходить от одних элементов к другим.

Например, пусть имеется элемент 3И-НЕ, а необходимо реализовать следующие операции:

     1. НЕ

     2. И (для 2-x переменных)

     3. ИЛИ (для 2-x переменных)

Реализуем эти операции.

1.  Операция НЕ получается на основании закона тавтологии (рис.1.15)

                                                 

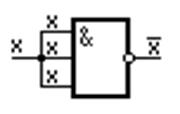
                     Рисунок 1.15 – Инвертор на элементе Шеффера

2. Операция  И  получается на  основании законов тавтологии и двойного отрицания (рис. 1.16)

                                        

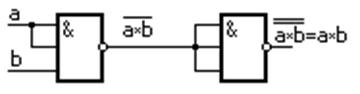
              Рисунок 1.16 – Конъюнктор на элементах Шеффера

3. Операция  ИЛИ получается на основании правила двойственности, когда искусственно выполняют двойное отрицание, которое не меняет значение ФАЛ и нижнюю черту (отрицание) преобразуют по правилу Моргана 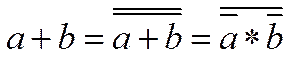 . Тогда получаем следующую реализацию (рис. 1.17):

                                      

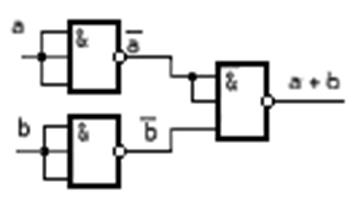
      Рисунок 1.17 –Дизъюнктор на элементах Шеффера

                 1.3 Формы представления функций алгебры логики

Функции алгебры логики могут быть заданы различными способами:

           -  таблицей истинности 

           -  в аналитической форме

           -  в числовой форме.

Таблица истинности уже была рассмотрена. В ней все наборы логических переменных следуют строго в порядке  возрастания их двоичного номера и нумеруются целыми  числами  от  0  до 2 ⁿ - 1, где n – число переменных функции.

Если функция имеет значения на всех наборах, то она называется полностью определенной.

При аналитической записи используются так  называемые  нормальные формы.

Для лучшего понимания материала введем некоторые понятия:

             *  терм - компонент выражения;

             *  ранг терма - число переменных, входящих в терм;

             * элементарная дизъюнкция - дизъюнктивный терм или  макстерм - это  дизъюнкция произвольного числа попарно независимых переменных. Например, 

                            

                             

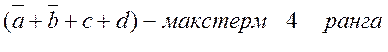
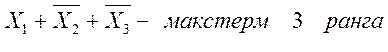
                              это не макстерм т.к. переменные  a  и    попарно

                                                     зависимые.

             * элементарная конъюнкция - конъюнктивный терм  или  минтерм  - конъюнкция  произвольного числа попарно независимых переменных. Например,               

                       Х ₁Х ₂ Х₃ - минтерм 3-его ранга

                          –   это не минтерм, так как переменные  и     зависимые.

Для аналитической записи функций используют две  формы:

         1) Дизъюнктивную Нормальную Форму - ДНФ

         2) Конъюнктивную Нормальную Форму - КНФ

      ДНФ  это  дизъюнкция  минтермов различного ранга

                                        

      КНФ  это  конъюнкция макстермов различного ранга