Цифровые устройства и микропроцессоры: Учебное пособие, страница 16

 Запятая в коде не пишется. Число нуль в прямом коде имеет двойное изображение – положительное и отрицательное.

Обратный код

                                                   

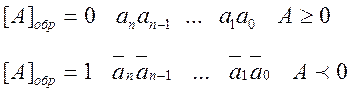
где   дополнение числа до 1  (инверсия разрядов двоичного числа).

                    Например,        Число               Обратный код

+ 1101	01101
- 1101	10010
- 0,1101	10010
+ 0,0000	00000

Дополнительный код

                                                   

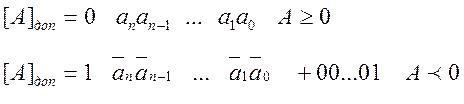
       где   дополнение числа до 1  ( инверсия разрядов двоичного числа).

Дополнительный код  числа это обратный код  плюс  единица в младший разряд.

Например,  

                                Число        Дополнительный   код

+1101	01101
- 1101	10011
- 1100	10100

Дополнительный код правильной дроби  – это дополнение числа до основания системы счисления.   , где 10 – основание системы счисления.

Дополнительный код   n – разрядного целого отрицательного числа есть результат вычитания этого  числа из единицы  с  (n+1) нулями. Так,  для числа    А = - 1101

 (n = 4)    .

Для положительных чисел  прямой,   обратный  и  дополнительный коды  совпадают.

2.6  Операции над числами в машинных кодах

Операции с фиксированной запятой

Сложение чисел.

В вычислительной технике, благодаря машинным кодам, операция вычитания  заменяется операцией сложения с числом обратного знака.

                                          

Сложение в обратном коде.

Пусть даны два числа  А и В. Надо найти их сумму.

                                                

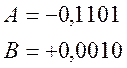
Выполним сложение в обратном коде.  При этом биты знака участвуют в сложении наравне со значащими разрядами

                                                                         

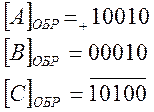
      Ответ:          

Теперь сложим два других числа

                                             

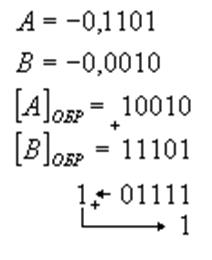
При сложение в обратном коде единица переноса из старшего  (знакового) бита добавляется в младший разряд результата - имеет место, так называемый, циклический перенос. Результат сложения    ,  а  ответ  С = - 0,1111                                                 

Сложение в дополнительном коде.

Выполним сложение тех же чисел

                                    

Теперь возьмём другие числа

                                                       

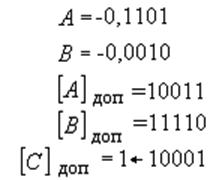
В дополнительном коде единица переноса из знакового бита отбрасывается. Тогда , а ответ  равен  С = - 0,1111.

При сложении  обязательно выравнивание   разрядов слагаемых  нулями (не кодов!). Для отрицательных чисел эти выравнивающие нули превращаются в единицы при инвертировании. Знаки чисел (крайние левые биты кодов) обязательно находятся один под другим.

Аналогично складывают и целые числа. Например, сложить в разрядной сетке 1 байт два числа   С = А + В, где  А= + 9  и  В = - 7. Разместим их  в фиксированной разрядной сетке – в восьми битах

                                  [А]пр   = 0 0 0 0 1 0 0 1

                                  [B]пр   = 1 0 0 0 0 1 1 1

                                  [A]доп = 0 0 0 0 1 0 0 1

                                  [В]доп = 1 1 1 1 1 0 0 1

                                  [С]доп = 0 0 0 0 0 0 1 0

                                  [С]пр   = 0 0 0 0 0 0 1 0

В результате сложения получилось положительное число, поэтому других преобразований ответ не требует.            

Умножение двоичных чисел.

Умножение выполняется по тем же правилам , что и десятичное умножение, то есть перемножаются модули чисел, а знак результата  получается сложением по модулю два  знаков сомножителей.

Известно,  что  произведение двух   n-разрядных чисел есть число 2n-разрядное

                                               

Возьмем  два  целых, четырёхразрядных  двоичных  числа

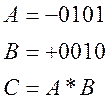                                                    ( n = 4 )