Цифровые устройства и микропроцессоры: Учебное пособие, страница 19

В некоторых машинах для контроля   переполнения  используют,   так называемые,  модифицированные  коды:  прямой,  обратный, дополнительный. В этих кодах под знак числа отводится по два бита. После сложения эти знаковые биты складывают между собой по модулю два. Если результат сложения равен 0, то нет переполнения, если результат сложения равен 1, то переполнение есть. Проверим это правило на примере обратного модифицированного кода. Сложим два числа:

                                                           

                      

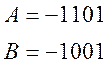
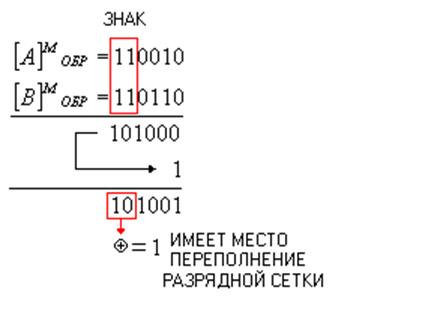
Таким образом, модифицированные коды удобны для использования, хотя и занимают на один бит больше памяти.

2.9  Контроль информации

Рассмотренные  ранее  алгоритмы  выполнения  операций  дают правильный результат, если не будет сбоев в работе  машины.  Если произойдет сбой, то ответ будет неправильный и  пользователь никогда об этом не узнает, поэтому в первых вычислительных  машинах  всегда выполнялся двойной счет. В  современных  машинах  существуют специальные системы контроля, которые  позволяют определить   наличие ошибки и даже автоматически ее исправить. Вообще система контроля это совокупность средств и методов, обеспечивающих проверку правильности работы устройства , обнаружение и исправление ошибок.

Простейшим методом контроля  является  проверка  на  четность  (проверка  паритета). Исходное число дополняют битом четности, в который заносят 0  или 1 с тем, чтобы общее количество единиц было четным (рис.2.8).

Число	Бит паритета	Код
1010	0	10100
1000	1	10001
0010	1	00101

                                Рисунок 2.8 – Добавление бита паритета

Этот метод позволяет выявить только одну ошибку. Кодировка и проверка выполняются автоматически с помощью сумматоров по модулю два (рис. 2.9).

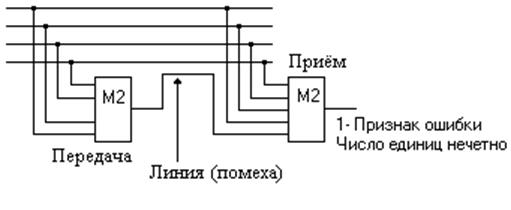
Рисунок 2.9 – Проверка паритета в месте приёма

Для автоматического исправления ошибки этот метод видоизменяют – добавляют   несколько контрольных разрядов по типу матрицы (рис. 2.10):

M1	M2	M3	K1
M4	M5	M6	K2
M7	M8	M9	K3
K4	K5	K6

                 Рисунок 2.10 – Добавление битов паритета в матрицу

       Здесь         M – информационные  разряды

                          K – контрольные разряды  

                          N=M+K=9+6=15 – общее число разрядов кода

Проверку на четность выполняют по строкам и по столбцам. Одиночная ошибка сразу выявляется и исправляется  (рис. 2.11).

0	1	1	0
1	0	1	0
0	0	0	1 ?
1	0 ?	0

                        Рисунок 2.11 – Исправление ошибки в матрице

Кодирование по методу четности  -  довольно  мощный  и  надежный способ защиты информации. Такие узлы находят применение на практике.

Для более длинных посылок или обнаружения двух и более ошибок используют и более сложные коды,  например, коды Хемминга.

2.10 Представление алфавитно – цифровой информации

С помощью двоичных  знаков можно записывать, хранить и обрабатывать не только числа, но и любую символьную информацию. Для этого каждому символу необходимо присвоить свой код. С помощью кода, состоящего из n – разрядов, можно представить  2ⁿ  различных символов. В 1963 году был введён  7 – разрядный   код   ASCII  (American Standard Code for Information Interchange  - американский стандартный код для обмена информацией). Он позволял кодировать 128 символов. На основе этого кода построен отечественный код  КОИ – 7 и  восьмиразрядные коды КОИ – 8 и ДКОИ (двоичный код обработки информации), в которых каждый символ кодируется одним байтом. Последующие модификации кода ASCII также 8 – разрядные (байтовые). Поэтому  можно закодировать 256 различных символов. Например, разряды байта кода ДКОИ  распределяются следующим образом: