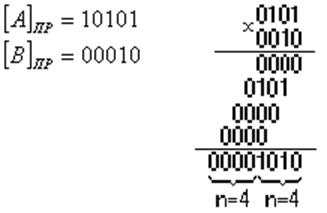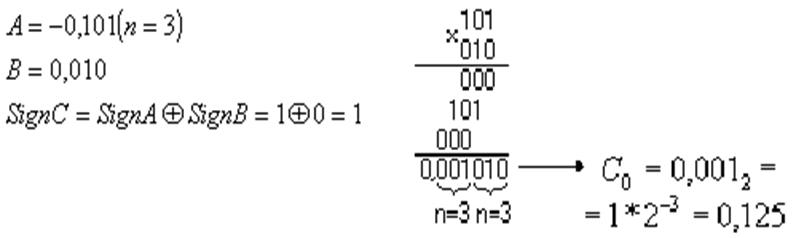Цифровые устройства и микропроцессоры: Учебное пособие, страница 17

Знак произведения  . Перемножаем модули                                                                                         

При умножении целых чисел в качестве результата  берутся  младшие n-разрядов. При этом  в старших n-разрядах должны быть нули.  Если это не так, то имеет место переполнение разрядной сетки машины. Для расширения разрядной сетки нужно добавить слева нули. Теперь умножим два дробных числа:

При  умножении дробных  чисел  в  качестве  результата  выбираются старшие n-разрядов. При этом происходит округление по правилу:  если  в  (n+1) разряде была единица, то к ответу добавляется единица  в  младший разряд,  если  в  (n+1)  разряде, был ноль, то к ответу ничего не добавляется. В примере имеем ноль, поэтому ничего не добавляем. Проверим ответ в десятичной системе:

                             

                             

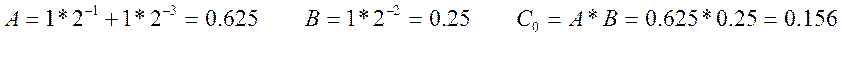
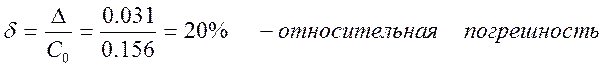
Округление при умножении дробных  чисел  вносит значительную  погрешность (операции же с целыми числами  выполняются  абсолютно точно!).     Погрешность, возникающая при умножении дробных чисел равна

                          

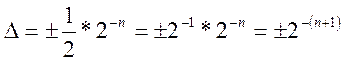
Чтобы не потерять точность при вычислениях, нужно расширить разрядную сетку путём  добавления нулей справа.

Операции с плавающей запятой.

Операции над числами с плавающей запятой выполняются по тем же правилам. Мантиссы отрицательных чисел вступают в операцию в обратном или дополнительном коде.  Перед  сложением чисел сначала выравнивают порядки – приводят число к большему порядку и затем складывают мантиссы. Полученный результат нормализуют. Для умножения чисел перемножают мантиссы по правилам двоичной арифметики, а порядки складывают.

В качестве примера,  рассмотрим сложение  двух действительных десятичных чисел  А = 3,23  и  В = - 14,85  в классическом формате с плавающей запятой, используя дополнительный код .    С = А + В = ?

Решение начнём с перевода чисел в двоичную систему счисления.

 А = 3,23= + 11, 0011101= + 0,110011101 * 2

 В = - 14,85= - 1110,1101100= - 0,11101101100 * 2

Количество разрядов после запятой в ненормализованном двоичном числе равно  n= n/ 0,3 = 2 / 0,3 = 7

Занесём эти числа в разрядную сетку 4 байта

                [А]пр   = 0 110011101000000000000000 0 000010

                [B]пр   = 1 111011011000000000000000 0 000100

 Приводим  операнды  к  большему порядку (4  = 100 ) 

                [А]пр   = 0 001100111010000000000000 0 000100

 Записываем дополнительные коды операндов

                [B]обр  = 1 000100100111111111111111 0 000100               

                [B]доп  = 1 000100101000000000000000

                [А]доп  = 0 001100111010000000000000

                [С]доп  = 1 010001100010000000000000 – результат сложения

                [С]обр  = 1 010001100001111111111111

                [С]пр    = 1 101110011110000000000000 0 000100

           Ответ в двоичной системе счисления:    С = - 0,10111001111 * 2= - 1011,1001111= -(2+ 2 + 2+ 2 +2+ 2 + 2 + 2)  - 11,617

 Точный ответ С= - 14,85 + 3,23 = - 11,62. Появилась погрешность за счёт перевода  чисел в двоичную систему счисления.

2.7 Двоично – десятичная система кодирования

Все операции в ЭВМ выполняются в двоичной системе счисления. Однако человеку удобно вводить информацию и получать результаты вычислений в десятичной системе счисления.  Для этого используются, так называемые, двоично-десятичные коды. В них один десятичный разряд представляют  четырьмя двоичными разрядами (тетрадой). При помощи четырех бит можно закодировать шестнадцать различных символов (цифр). Существует много разных систем кодирования [1…5], но наиболее широко применяется код 8–4–2–1 (это веса двоичных разрядов влево от запятой). Составим таблицу соответствия двоично-десятичного кода и десятичных цифр: