Цифровые устройства и микропроцессоры: Учебное пособие, страница 10

       2)  графическим путем (метод карт Карно или диаграмм Вейча), используя специальные карты,

      3)  расчетно-графическим путем (метод Квайна и его модификации).

Расчетный метод мы уже разобрали выше. Метод карт Карно хорошо работает при числе переменных меньше шести, прост и удобен для  оперативного использования. Тем более, что большинство устройств, с которыми имеет дело разработчик, оперирует именно с малым числом переменных (3…5). Он подробно описан в литературе [2,5,6]. Метод Квайна используется при  числе переменных больше шести, хорошо алгоритмизируется и программируется. На его основе разработаны системы автоматизированного проектирования и  стандартные программы минимизации логических функций любого числа переменных. Но они не всегда доступны и  не оправданы при малом  числе независимых переменных.

1.4.2  Примеры минимизации

Пример 1.

Найти МДНФ такой функции:  F(a,b,c)=V(1,3,6,7) . Составим её таблицу истинности, которая приведена на рис. 1.21

№\X	a	b	c	f
0	0	0	0	0
1	0	0	1	1
2	0	1	0	0
3	0	1	1	1
4	1	0	0	0
5	1	0	1	0
6	1	1	0	1
7	1	1	1	1

                         Рисунок 1.21 – Таблица истинности функции

Запишем СДНФ исходной функции и преобразуем её по законам алгебры логики (вынесением за скобку) .  Получили МДНФ.

Пример 2.

Минимизировать функцию трёх переменных:   F(a,b,c)=  (0,4,5).

Начинаем с составления таблицы истинности (рис. 1.22)

№\X	a	b	c	F
0	0	0	0	0
1	0	0	1	1
2	0	1	0	1
3	0	1	1	1
4	1	0	0	0
5	1	0	1	0
6	1	1	0	1
7	1	1	1	1

                            Рисунок 1.22 –  Таблица истинности

Составим СДНФ и выполним склеивание минтермов  (конституент единицы) каждого с каждым: 

                                    

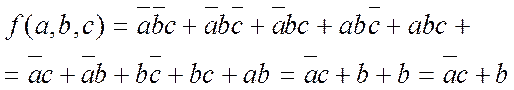
Первый склеиваем  со вторым , затем с третьим, с четвёртым и т.д. Далее второй склеиваем с третьим, с четвёртым и т.д. Все минтермы пройдут через склеивание. После первого склеивания выполняется второе и т.д. пока оно возможно. Напомним, что минтермы для склеивания могут отличаться только одной переменной.

Пример 3.

Минимизировать функцию  двух  переменных, заданную в виде формулы:

 / сначала приведем логическую формулу к нормальному виду - (СДНФ) /  =      

Путём склеивания  минтермов  получаем

                                                       . 

Пример 4.

Минимизировать функцию четырёх переменных,  заданную такой СДНФ

         / выполняем поочерёдное склеивание минтермов, каждого с каждым /=/ снова склеиваем  минтермы / =     Тогда  имеем минимальную форму

                                               

Её схемная реализация на произвольных элементах имеет вид (рис.1.23):            

                                            

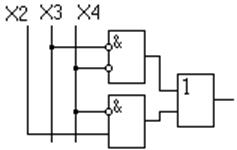
              Рисунок 1.23 – Схемная реализация функции четырёх переменных

1.4.3. Минимизация не полностью определенных функций

Имеется ряд функций, значение которых на некоторых наборах неопределено  или нас просто не интересует. Такие наборы называются запрещенными и используются для минимизации, дополняя функцию нулями или единицами так, чтобы провести куб более высокого ранга.

Пусть, например, имеем функцию трёх переменных, заданную такой таблицей истинности (рис.1.24):