Вполне очевидно, что для записи одного и того же числа в разных системах счисления требуется разное количество разрядов. Основание системы счисления во всех системах счисления записывается одинаково: 10.
2.2 Перевод чисел из одной системы в другую
Перевод целых чисел и правильных дробей выполняется по разным правилам. В действительном числе переводят отдельно целую и дробную части.
Перевод целых чисел.
Для перевода необходимо исходное число разделить на основание новой системы счисления до получения целого остатка, который является младшим разрядом числа в новой системе счисления. Полученное частное снова делим на основание и так до тех пор, пока частное не станет меньшего нового основания. Все операции выполняются в исходной Ссч.
Например, перевод из десятичной в двоичную и восьмеричную системы счисления.
Возьмём десятичное число А = 124
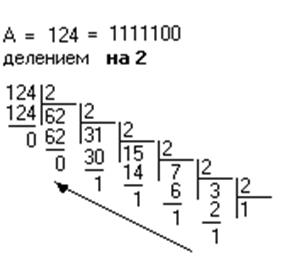
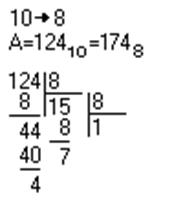
Аналогично переходим 10
16
А = 124
= 7С
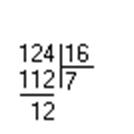
Перевод 8 2 также
выполняем делением
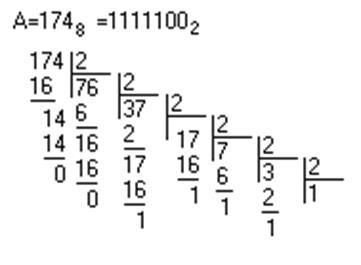
Однако выполнять деление в восьмеричной системе не всегда удобно (подсознательно мы делим в десятичной Ссч!!), поэтому используют более простое правило: каждую восьмеричную цифру представляют триадой двоичных
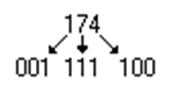
Аналогично делают обратный перевод, т.е.
двоичное число разбивают на триады относительно крайнего правого разряда (или
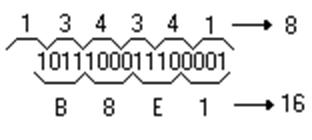
запятой) и каждую триаду представляют восьмеричной цифрой. Перевод 16 2 выполняют с помощью тетрад
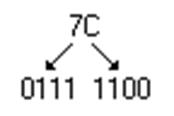
Перевод из двоичной системы счисления в 8-ую и 16-ую и обратно выполняется также.
Перевод правильных дробей.
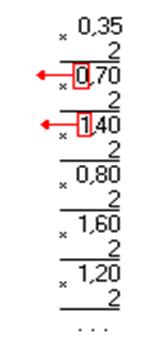
Этот перевод выполняется умножением исходного числа на основание новой системы счисления. Целая часть произведения является старшим разрядом числа в новой системе счисления. Дробную часть произведения снова умножают на основание системы счисления и т.д. Все операции выполняют в исходной Ссч.
Перевод 
В общем случае перевод правильных дробей является бесконечным. Число разрядов в новой системе можно найти исходя из одинаковой точности представления чисел в разных системах счисления.
Одинаковая точность – одинаковые веса младших разрядов чисел.
,
где p и q - основания старой и новой Ссч соответственно.
Например, для десятичного числа 0.35 вес младшего
разряда 1/ 100 = 0.01, а для двоичного числа 0.01011 вес младшего разряда
1/ 32 
0.03.
Берем логарифм по основанию p:
, откуда находим 
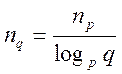
Тогда при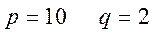 
получаем
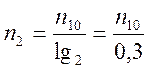
Если 
, то
в новой Ссч количество разрядов равно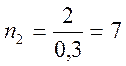 
а
при 
, 
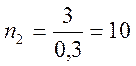. Для восьмеричной и шестнадцатеричной Ссч имеем
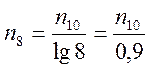
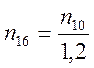
Из 10-й в 8-ую Ссч переходим по тому же правилу:
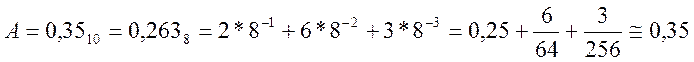
Аналогично можно делать перевод в любую систему
счисления. Перевод из 
и назад выполняется с
помощью триад и тетрад, которые отмеряют от запятой.
2.3 Арифметические операции в различных системах счисления
Арифметические операции в различных системах счисления выполняются на основании таблиц сложения и умножения.
Двоичная Ссч. Таблицы сложения и умножения.
0+0 = 0 0 * 0 = 0
0 +1 = 1 0 * 1 = 0
1 +0 = 1 1 * 0 = 0
1 +1 = 10 1 * 1 = 1
Возьмём два десятичных числа и выполним сложение, вычитание и умножение
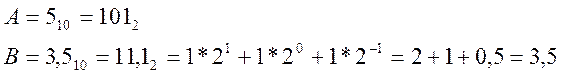
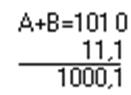
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.