Цифровые устройства и микропроцессоры: Учебное пособие, страница 11

№\X	a	b	c	F
0	0	0	0	*
1	0	0	1	1
2	0	1	0	1
3	0	1	1	0
4	1	0	0	1
5	1	0	1	*
6	1	1	0	1
7	1	1	1	0

      Рисунок 1.24 – Таблица истинности  не полностью определённой функции                                   

Здесь символом  *  обозначены запрещённые комбинации входных переменных.  Требуется найти минимальную форму.

Если не использовать запрещённые наборы, то минимальная форма после склеивания будет следующей:                                                

          .

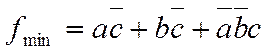Если на запрещённых наборах функцию дополнить единицами, то получаем такую СДНФ:

       

Минимальная форма     .  Очевидно, что  схемная реализация этой формулы  будет значительно  проще.

1.5  Синтез логических схем

1.5.1 Синтез схем с одним выходом

Синтез комбинационных схем с одним выходом включает следующие этапы:

      1)   Кодирование входных и выходных переменных и переход от словесного описания работы устройства  к таблице истинности.

      2)   Получение СДНФ.

      3)   Минимизация функции.

      4)   Перевод минимальной формы на заданные элементы (при необходимости).

      5)   Составление логической схемы.

Рассмотрим все эти этапы на примере.

Имеется три датчика, выходные сигналы которых двоичные числа.

Используя элементы Шеффера 2И-НЕ, обеспечить индикацию на выходе, если, по меньшей мере, два  из трёх входных сигналов единичны. Выполняем кодировку и составляем таблицу истинности (рис.1.25):

№\X	a	b	c	f
0	0	0	0	0
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	0
5	1	0	1	1
6	1	1	0	1
7	1	1	1	1

               Рисунок 1.25 – Таблица истинности исходной функции

Записываем СДНФ: .     

Путём склеивания минтермов получаем  МДНФ и преобразуем  к виду  И - НЕ:                

Схемная реализация этой функции выглядит следующим образом (рис. 1.26)

                                                                                                        

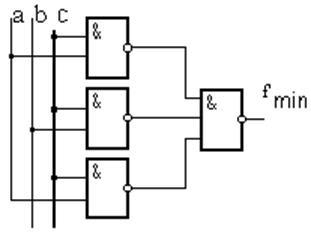
                               Рисунок 1.26 – Схемная реализация функции  (рис. 1.25)

Однако, эта схема не отвечает условиям задачи, так как использует трёхвходовой  элемент Шеффера. Требуется преобразовать функцию под двухвходовые элементы. Снова воспользуемся двойным отрицанием, которое не меняет значения функции, но объединяет по два входа

                                         

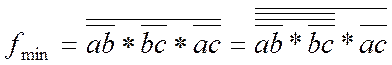
Последнее выражение реализуется уже на двухвходовых элементах (рис. 1.27)

                                           

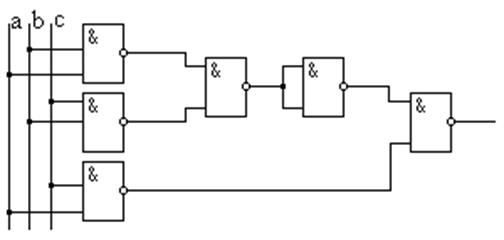
                 Рисунок 1.27 – Схемная реализация функции  (рис. 1.25)

                                           на двухвходовых элементах

  Условия задачи выполнены.

1.5.2  Синтез схем с несколькими выходами

Если логическая схема имеет n входов (n  число независимых переменных) и по условию задачи должна иметь k выходов, то каждый из k выходов описывают своей функцией алгебры логики.

                                     

                                              

                                      

                                    

Эта система функций называется системой собственных функций и описывает, так называемый,  логический  (n,k) – полюсник. Этапы  синтеза (n,k) – полюсников повторяют этапы синтеза схем с одним выходом, только каждую функцию минимизируют отдельно, хотя известно, что совместная минимизация дает лучшие результаты.