Цифровые устройства и микропроцессоры: Учебное пособие, страница 6

F\X	0	1	Название функции
F1	0	0	сonst “0”- абсолютно ложная функция
F2	0	1	переменная икс – тождественная функция
F3	1	0	“не икс” – отрицание икс – инверсия икс
F4	1	1	сonst “1” - абсолютно истинная функция

     Функция F₁ всегда равна нулю не зависимо от переменной Х. Функция  F₂  равна переменной  Х, функция F ₄  всегда равна 1 не зависимо от переменной Х. Функция F₃ (“не икс”) реализуется  инвертором, который изображён на рис.1.1

                                                                                                              

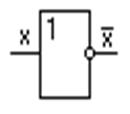
Рисунок 1.1 – Инвертор

     Если имеем  n-число независимых логических переменных, то можно составить 2ⁿ = N наборов этих переменных, а так как на каждом из наборов функция может принимать значение 0 или 1 , то общее  возможное число функций равно   L=2^N . Так, при n = 1 число наборов  N=2, а число функций L = 4.

      Рассмотрим логические функции двух переменных  n = 2 – элементарные функции. Число наборов N = 2²  =  4, а число функций L = 16.

     На практике используются не все  элементарныe функции, а значительно меньшее их количество.    Рассмотрим некоторые из них:

1.  Логическое умножение, операция “И” – конъюнкция. Выполняется элементом – конъюнктором (рис 1.2).

                                                                                                      

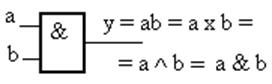
                                     Рисунок 1.2 -Конъюнктор

 Его таблица истинности     

№\X	а	b	y
0	0	0	0
1	0	1	0
2	1	0	0
3	1	1	1

                       Рисунок 1.3 – Таблица истинности конъюнктора

2.  Операция Шеффера “И – НЕ” – отрицание конъюнкции. Выполняется элементом Шеффера (рис. 1.4).

                                     

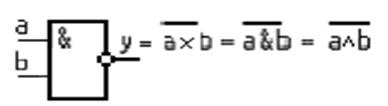
                                    Рисунок 1.4 – Элемент Шеффера

Его таблица истинности

№\Х	а	b	у
0	0	0	1
1	0	1	1
2	1	0	1
3	1	1	0

                Рисунок 1.5 -Таблица истинности элемента Шеффера

3. Логическое сложение, операция  “ИЛИ” – дизъюнкция. Выполняется элементом – дизъюнктором (рис.1.6).

                                      

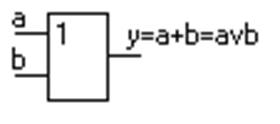
                                 Рисунок 1.6 – Дизъюнктор

Его таблица истинности

№\X	a	b	у
0	0	0	0
1	0	1	1
2	1	0	1
3	1	1	1

                     Рисунок 1.7 – Таблица истинности дизъюнктора

4.  Операция Пирса - отрицание дизъюнкции. Логическое “ИЛИ – НЕ”. Выполняется элементом Пирса (рис. 1.8).

                                      

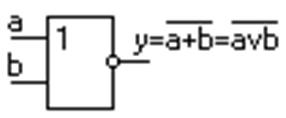
                                   Рисунок 1.8 – Элемент Пирса

Его таблица истинности

№\X	a	b	y
0	0	0	1
1	0	1	0
2	1	0	0
3	1	1	0

                   Рисунок 1.9 – Таблица истинности элемента Пирса

5. Логическая неравнозначность или сумма по модулю два  - М2.

Выполняется сумматором по “модулю два” (рис. 1.10). Функция истинна на тех наборах, где число единиц нечетно.