Пусть, например, требуется синтезировать ( 2 , 5 ) – полюсник, заданный
такой таблицей истинности
|
№\X |
a |
b |
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
2 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
|
3 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Рисунок 1.28 – Таблица истинности (2,5) – полюсника
Составляем систему собственных функций и минимизируем каждую из них:
![]()
![]()
![]()
![]()
![]()
На основании этих выражений составляем схему (рис. 1.29)

Рисунок 1.29 – Схемная реализация функции (рис. 1.28)
1.5.3 Скобочная форма функций алгебры логики
Пусть, в результате минимизации получена такая функция (МДНФ):
![]()
Построим схему, реализующую эту функцию (рис. 1.30)

Рисунок 1.30 – Схемная реализация исходной функции.
Время, через которое сигнал появляется на выходе
(задержка) 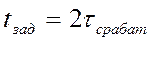 , где
, где
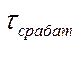 - время
прохождения сигнала через один элемент.
- время
прохождения сигнала через один элемент.
Функция, полученная в результате решения задачи минимизации, не является абсолютно минимальной и допускает дальнейшее упрощение путем вынесения за скобку общих множителей (так называемая скобочная форма).
![]()
Построим схему, реализующую эту функцию (рис. 1.31)
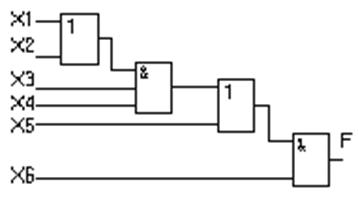
Рисунок 1.31 – Схемная реализация скобочной формы функции
Логическая формула получилась проще, общее число
входов меньше, но время задержки увеличилось и равно 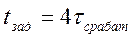 . Возросла “глубина” схемы и увеличилось время
прохождения сигнала. Поэтому, наиболее быстродействующие схемы это схемы
двухуровневые, построенные по ДНФ.
. Возросла “глубина” схемы и увеличилось время
прохождения сигнала. Поэтому, наиболее быстродействующие схемы это схемы
двухуровневые, построенные по ДНФ.
2 Арифметические основы электронно-вычислительных
устройств
2.1 Системы счисления
Система счисления (Ссч) – это совокупность правил записи чисел цифровыми знаками. Они бывают позиционные и непозиционные (например, римская Ссч). В вычислительной технике используются только позиционные системы счисления.
Число в любой позиционной Ссч можно представить в виде последовательности цифр:
![]() ,
,
где ai, bi – цифры данной системы счисления.
Или в виде формулы разложения
![]()
где p – основание системы счисления (количество различных цифр в Ссч)
pi – вес единицы данного разряда.
В ЭВМ используются системы счисления с основаниями p = 10, 2, 8, 16.
Рассмотрим эти системы счисления.
Десятичная Ссч.
р = 10 Разрешённые цифры (0,1,2,3,4,5,6,7,8,9). Число можно представить так
![]() . Веса соседних разрядов влево и вправо от запятой
различаются в десять раз ( р = 10 )
. Веса соседних разрядов влево и вправо от запятой
различаются в десять раз ( р = 10 )
…1000 100 10 1 , 1/10 1/100 1/1000 …
Двоичная Ссч.
р = 2 Разрешённые цифры (0,1) . Число представляется так
![]() = 46,625
= 46,625
Веса соседних разрядов влево и вправо от запятой различаются в два раза ( р = 2 )
… 32 16 8 4 2 1, 1/2 1/4 1/8 …
Восьмеричная Ссч.
р = 8 Разрешённые цифры (0,1,2,3,4,5,6,7) . Число представляется так
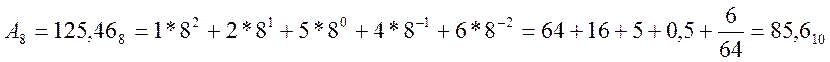 Веса соседних разрядов влево и вправо от запятой
различаются в восемь раз ( р = 8 )
Веса соседних разрядов влево и вправо от запятой
различаются в восемь раз ( р = 8 )
… 4096 512 64 8 1 , 1/8 1/64 1/512 ...
Шестнадцатеричная Ссч
р = 16 Разрешённые цифры (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F). Число представляется так
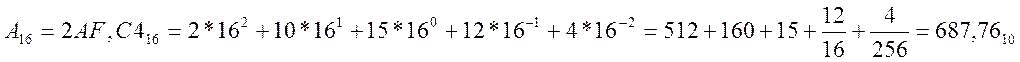 Веса соседних разрядов влево и вправо от
запятой различаются в шестнадцать раз (р=16 )
Веса соседних разрядов влево и вправо от
запятой различаются в шестнадцать раз (р=16 )
…4096 256 16 1, 1/16 1/256 1/4096 ...
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.