Цифровые устройства и микропроцессоры: Учебное пособие, страница 7

                                               

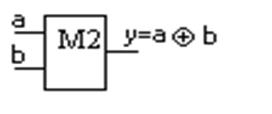
                                Рисунок 1.10 – Сумматор по модулю два

Его таблица истинности

№\X	a	b	y
0	0	0	0
1	0	1	1
2	1	0	1
3	1	1	0

             Рисунок 1.11 – Таблица истинности сумматора по модулю два

Вместе с тем, в литературе встречается функция, так называемая,                         “исключающее ИЛИ”, которая истинна, на тех наборах, где присутствует исключительно одна единица. Операция выполняется элементом  “исключающее ИЛИ” (рис.1.11)

                                            

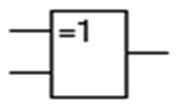
                   Рисунок 1.11 – Элемент  “исключающее ИЛИ”

Его таблица истинности

№\X	a	b	y
0	0	0	0
1	0	1	1
2	1	0	1
3	1	1	0

          Рисунок 1.12 – Таблица истинности элемента “исключающее ИЛИ”

Видно, что таблицы истинности совпадают. Значит для двух переменных функции  M2  и   =1  –  эквивалентны.

   Составим таблицу истинности этих функций при числе переменных  n = 3

№	a	b	c	M2	=1
0	0	0	0	0	0
1	0	0	1	1	1
2	0	1	0	1	1
3	0	1	1	0	0
4	1	0	0	1	1
5	1	0	1	0	0
6	1	1	0	0	0
7	1	1	1	1	0

          Рисунок 1.13 – Таблица истинности элементов    М2  и  =1

                                     для  трёх  переменных

Видно, что они различаются в последнем наборе. При большем числе переменных, количество строк, где функции различаются возрастает, поэтому функции М2  и  =1 нельзя отождествлять.

Графическое изображение и условное обозначение логических элементов регламентируются  ГОСТ 2.743-91 ЕСКД. Этот ГОСТ устанавливает следующие геометрические размеры (рис. 1.14):

                    

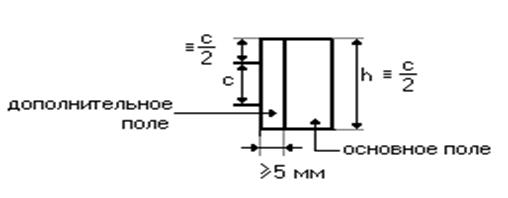
            Рисунок 1.14 – Условное изображение логических элементов

Величина С  5 мм. Других ограничений на размеры логических элементов ГОСТ не накладывает.

                                   1.2  Законы алгебры логики

Они базируются на аксиомах алгебры логики и позволяют преобразовывать логические функции.

           АКСИОМЫ алгебры логики:

                                   0 * 0 = 0                    0 + 0 = 0

                                   0 * 1 = 0                    0 + 1 = 1

                                   1 * 0 = 0                    1 + 0 = 1

                                   1 * 1 = 1                    1 + 1 = 1

1. Закон одинарных элементов

                                   1 * X = X                  0 * X = 0

                                   1 + X = 1                   0 + X = X

    2. Законы отрицания

       а) Закон дополнительных элементов.

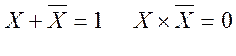
       б)  Закон двойного отрицания

                       

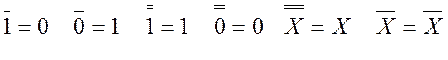
    поэтому отрицание можно переносить из одной части равенства в другую.

       в)  Закон двойственности (правилоМоргана).

                                 

Отрицание дизъюнкции есть конъюнкция отрицаний и наоборот - отрицание конъюнкции есть дизъюнкция отрицаний:

                             

Правило справедливо для любого числа переменных.

    3. Комбинационные законы.

   Они во многом соответствуют обычной алгебре, но есть и отличия.

а) тавтологии (многократное повторение)