Цифровые устройства и микропроцессоры: Учебное пособие, страница 18

Двоично-десятичный код				Десятичная цифра
8         4          2          1
0	0	0	0	0
0	0	0	1	1
0	0	1	0	2
0	0	1	1	3
0	1	0	0	4
0	1	0	1	5
0	1	1	0	6
0	1	1	1	7
1	0	0	0	8
1	0	0	1	9

Остальные комбинации двоичного кода являются лишними (запрещенными). Запишем пример двоично-десятичного кода:

1258    =        0001 0010    0101 1000

  589    =        0000 0101    1000 1001

Сложение двоично-десятичных чисел

Сложение двоично-десятичных чисел  производится по правилам двоичной арифметики, с учетом переносов. Пусть имеем два десятичных числа А и В. Требуется найти сумму  С = А + В.  

В  каждой тетраде  выполняется сложение трёх чисел  - двух слагаемых и переноса из предыдущего разряда,  т.е.  а_n  + b_n   + p_n-1.  При этом возможны такие ситуации.

1)  а_n  + b_n   + p_n-1    < 10 .      А = 14        В = 23      С = А + В = 37

    А  =  0001   0100

     В =  0010   0011

     С =  0011   0111      37       Ответ получился верный.

2) а_n  + b_n   + p_n-1    > 15 .       А = 47         В = 39      С = А + В = 86

     А = 0100     0111

     В = 0011     1001

     С = 1000 0000      80      Ответ  получился неверный, так как был перенос из младшей тетрады в старшую. Тетрада переполняется числом 16, т.е. единица межтетрадного переноса уносит в старшую тетраду 16 , а не 10 единиц как в десятичной системе счисления ( шесть лишних единиц! ). Поэтому результат необходимо скорректировать путём добавки  + 6.  Выполним коррекцию

      С = 1000   0000

             0000   0110     -   коррекция  (+ 6)

ответ            1000   0110         86        Ответ  правильный.

      3)  10  а_n  + b_n   + p_n-1    15           А = 47       В = 36     С = А + В =83

                    А = 0100   0111

                    В =  0011  0110

                    С =  0111  1101           Ответ неверный, хотя и нет межтетрадного переноса, но имеется запрещённая комбинация. Необходимо вызвать искусственное переполнение тетрады  путём добавки +6. Выполним коррекцию

                     С = 0111   1101

                            0000   0110     -     коррекция  ( + 6)

     ответ             10000011       83       Теперь ответ  правильный. Внимание! Коррекция результата выполняется только один раз, поэтому межтетрадный перенос при коррекции  не требует ещё одной коррекции.

Таким образом, при сложении двоично – десятичных  чисел выполняется   коррекция результата по правилу – если был межтетрадный перенос (переполнение тетрады) или получилась запрещённая комбинация, то к этой тетраде добавляется + 6 (0110).  

    Ещё один пример.      А = 479         В =   128       С = А + В =  607  

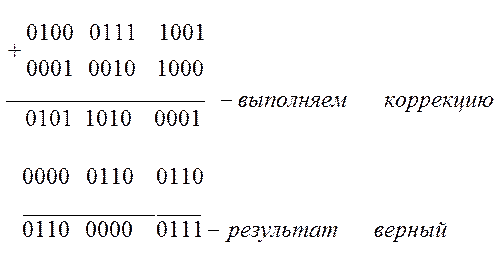
В старшей тетраде коррекция  0, в средней -  +6 (запрещённая комбинация), в младшей тетраде   +6 ( был перенос ).

2.8  Переполнение разрядной сетки машины

     При сложении чисел одинакового знака может возникнуть переполнение разрядной сетки. Признаком переполнения является отличие знака результата от знаков слагаемых.  Пусть,  например, требуется сложить два числа:

                               

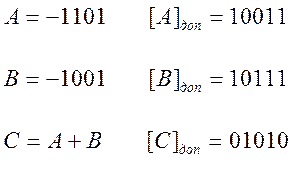
Складывали два отрицательных числа , а ответ – положительный. Чтобы не было переполнения необходимо расширить разрядную сетку.      Запишем числа  A  и  B  в пяти битах

                 

                                                                

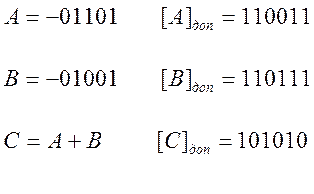
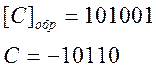
Теперь ответ верный. В вычислителях для контроля    переполнения  следят за переносом в знаковый разряд и из него. Если оба переноса имеют место или оба отсутствуют, то переполнения нет. Если есть хотя бы один из переносов, то имеет место переполнение разрядной сетки.