Перепишем равенство (12.11) в виде
G(x)P(x) = Q(x)xr + R(x).(12.12)
Левая часть (12.12) делится без остатка на Р(х), значит без остатка делится и правая часть. Из (12.12) вытекают два способа формирования комбинаций циклического кода: путем умножения многочлена G(x) на Р(х) и путем деления Q(x)xr на Р(х) и приписывания к Q(x)xrостатка от деления R(x).
Пример 12.5. Задан полином G(x) = х3 + х, соответствующий комбинации простого кода. Сформируем комбинацию циклического кода (7,4) с производящим полиномом Р(х) = = х3 + х2 + 1. Можно получить комбинацию циклического кода в виде G(x)P(x) = (х3 + х) (х3 + х2 + 1) = х6 + х5 + + х4 + х. Однако в полученной комбинации нельзя отделить информационные элементы от проверочных, и код получается неразделимым.
Перейдем ко второму способу, который чаще всего применяется на практике. Проделаем необходимые операции по получению комбинации циклического кода:
1) G(x)xr= (х3 + х)х3 = х6 + х4;
2) Х6+х4 Iх3+х2+1 х6+х5+х3 \х3+х2+\
х5+х4+х3
х5+х*+х2 '
х3+х2
х3+х2+1
R(x)=1
3) (х6 + х4 + 1) — комбинация циклического кода, полученная методом деления на производящий полином. Она может быть переписана в виде 1010001. Первые четыре элемента — информационные, последние три — проверочные, т.е. полученный код — разделимый.
Для обнаружения ошибок в принятой кодовой комбинации достаточно поделить ее на производящий полином. Если принятая комбинация разрешенная, то остаток от деления
будет нулевым. Ненулевой остаток свидетельствует о том, что принятая комбинация содержит ошибки. По виду остатка (синдрома) можно в некоторых случаях также сделать вывод о характере ошибки и исправить ее.
Циклические коды достаточно просты в реализации, обладают высокой корректирующей способностью (способностью исправлять и обнаруживать ошибки) и поэтому рекомендованы МСЭ-Т для применения в аппаратуре ПД. Согласно рекомендации V.41 в системах ПД с ОС рекомендуется применять код с производящим полиномом Р(х) = х16 + х12 + х5 + 1.
Эффективность применения корректирующих кодов. Полезный эффект от применения корректирующих кодов заключается в повышении верности. Вероятность неправильного приема кодовой комбинации простого кода определяется как вероятность появления в кодовой комбинации хотя бы одной ошибки, т.е.
где рош — вероятность неправильного приема единичного элемента; k— число элементов в комбинации простого кода. При применении систематических корректирующих кодов к исходной кодовой комбинации добавляются проверочные элементы, позволяющие исправлять или обнаруживать ошибки. Так, если код используется в режиме исправления ошибок и кратность исправляемых ошибок tи.ош, то вероятность неправильного приема кодовой комбинации
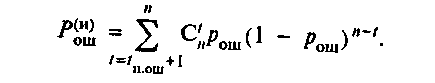
В результате применения корректирующего кода в режиме исправления ошибок
вероятность ошибки уменьшается в Кк раз: 
> 1- Однако это достигается за счет увеличения затрат на
реализацию системы и снижения скорости передачи информации. Если в системе с
простым кодом скорость равна Сп, то в системе с корректирующим кодом скорость Ск
= Сп • 
где = k/n— коэффициент, харак-
|
|
теризующий потери скорости вследствие введенной в код избыточности. Чем больше избыточность (меньше yt), тем меньше скорость передачи информации, т.е. тем меньше в единицу времени передается полезной информации.
Качество реальных каналов во времени меняется, и если заданы требования на верность передачи, то необходимо ввести такую избыточность, которая обеспечивала бы заданную верность даже при самом плохом качестве канала. Напрашивается мысль о целесообразности изменения избыточности, вводимой в кодовую комбинацию, по мере изменения характеристик канала связи. Системы, в которых меняется избыточность с изменением качества канала, относятся к числу адаптивных. Одним из типов адаптивных систем являются системы с обратной связью. В этих системах между приемником и передатчиком помимо основного (прямого) канала имеется вспомогательный (обратный).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
