Главный недостаток такого способа — существенное уменьшение скорости передачи. В нашем примере скорость передачи информации уменьшается в 5 раз по сравнению со случаем однократной передачи кодовых комбинаций.
Способ повышения верности, основанный на снижении скорости передачи, широко применяется в технике передачи дискретных сообщений. Так, в среднескоростных системах ПД с частотной модуляцией предусмотрены две скорости — 600 и 1200 Бод. Очевидно, что передача со скоростью 600 Бод равносильна передаче 2 раза подряд единичных элементов длительностью 1/1200 мс.
При одновременной передаче кодовой комбинации по нескольким параллельным каналам (обычно число каналов нечетное) решение о том, какая кодовая комбинация передавалась, выносится методом голосования (т.е. так же, как и при многократной передаче кодовых комбинаций). Иногда передача осуществляется по двум параллельным каналам, и информация выбирается из того канала, качество которого в момент приема кодовой комбинации было наилучшим. Для этого приемник должен располагать соответствующим устройством для оценки качества канала.
При передаче сообщений по N параллельным каналам скорость передачи информации не зависит от числа каналов. Однако при этом существенно возрастают (в N раз!) расходы на аренду каналов.
Более эффективно используются дискретные каналы при применении корректирующих кодов. В однонаправленных системах это должны быть коды, исправляющие ошибки. Широкое распространение на практике получили двоичные корректирующие коды, т.е. коды, при формировании которых используются только два типа элементов: 0 и 1. Только такие коды и будут рассматриваться в данной главе.
Построение корректирующих кодов. Каждому символу исходного алфавита сообщений объема Naпоставим в соответствие n-элементную двоичную последовательность — кодовую комбинацию. Возможное (общее) число последовательностей длины n составляет N0 = 2", причем должно соблюдаться условие
N0> Na.
Если N0 = Na , то все возможные последовательности п-элементного кода используются для передачи или, как говорят, являются разрешенными. Полученный таким образом код называется простым.
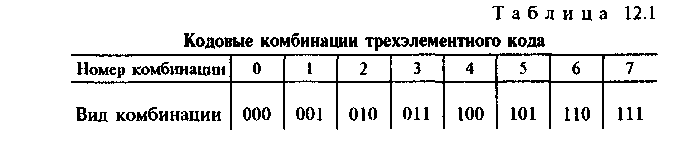
Пример 12.1. Для передачи сообщений, число которых равно восьми (Na= 8), используется трехэлементный код. Число кодовых комбинаций, которое можно при этом получить, N0= 23 = 8. Из табл. 12.1 видно, что комбинация под номером 0 отличается от комбинации 1 только в одной позиции. Следовательно, если при передаче комбинации 000
произойдет ошибка в третьем элементе, то получим комбинацию 001.
Степень различия комбинаций определяется расстоянием Хемминга d. Это расстояние для любых двух кодовых комбинаций определяется числом несовпадающих в них разрядов. Например, две ниже написанные друг под другом комбинации не совпадают в двух разрядах:
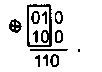
поэтому расстояние Хемминга d= 2. Иначе его
определяют как вес суммы по модулю два (
— условное обозначение суммы) этих кодовых
комбинаций. Весом Wкодовой комбинации называется
число входящих в нее ненулевых элементов. Перебрав все возможные пары кодовых
комбинаций, можно найти минимальное хеммингово расстояние, которое принято называть кодовым и
обозначать d0. Для примера 12.1
кодовое расстояние dQ= 1. Рассмотренный в примере код простой. Любая ошибка (даже одиночная!) при использовании такого кода приведет к тому, что переданная разрешенная кодовая комбинация перейдет в другую разрешенную. Таким образом, простой код не способен обнаруживать и тем более исправлять ошибки и имеет dQ= 1.
Для того чтобы код мог обнаруживать ошибки, необходимо соблюдение неравенства Na < N0. При этом неиспользуемые
n-элементные кодовые комбинации. число которых (N0 - Na), будем называть запрещенными. Они определяют избыточность кода. Очевидно, что появление ошибки в кодовой комбинации будет обнаружено, если переданная разрешенная комбинация перейдет в одну из запрещенных. В качестве
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
