Код Хемминга. Рассмотрим в качестве примера построение систематического кода с кодовым расстоянием do= 3 (кода Хемминга). Пусть число сообщений, которое необходимо передать, равно 16. Тогда необходимое число информационных элементов k = log2Na = 4. Можно выписать все 16 кодовых комбинаций, включая нулевую (0000). Это один из возможных способов задания исходного (простого) кода. Другой способ заключается в выписывании только четырех кодовых комбинаций простого кода в виде матрицы, называемой единичной:
Суммируя по модулю два в различном сочетании кодовые комбинации, входящие в единичную матрицу,
можно получить 15 кодовых комбинаций, 16-я —
нулевая. Кодовые комбинации,
составляющие матрицу (12.1), линейно независимы. Можно было бы составить матрицу и из других кодовых комбинаций (лишь бы они были линейно независимыми).
Ненулевые комбинации А1, А2, Л3, А4
линейно независимые, если q1A1![]()
![]() q2A2
q2A2![]() q3А3
q3А3 ![]() q4A4 ≠ 0, где qi
q4A4 ≠ 0, где qi![]() {0,1} при условии, что хотя бы один из
коэффициентовqi ≠ 0. Дополним каждую кодовую комбинацию в (12.1) проверочными элементами так, чтобы
обеспечивалось do= 3. Будем иметь в виду также тот факт,
что к числу разрешенных комбинаций корректирующего кода принадлежит и комбинация
0000 ... 0,
{0,1} при условии, что хотя бы один из
коэффициентовqi ≠ 0. Дополним каждую кодовую комбинацию в (12.1) проверочными элементами так, чтобы
обеспечивалось do= 3. Будем иметь в виду также тот факт,
что к числу разрешенных комбинаций корректирующего кода принадлежит и комбинация
0000 ... 0,
называемая нулевой. Очевидно, что в числе добавляемых проверочных элементов должно быть не менее двух единиц. Тогда общее число единиц в каждой комбинации кода получим не меньше трех и комбинации, полученные нами, будут отличаться от нулевой, по крайней мере, в трех элементах. Добавим по две единицы к каждой строке матрицы (12.1):
видим, что они отличаются только в двух элементах, т.е. заданное кодовое расстояние не обеспечивается. Дополним каждую строку проверочными элементами так, чтобы do= 3.
Тогда матрица примет вид
Добавляемые проверочные элементы могут быть записаны и в другом порядке. Необходимо лишь обеспечить do= 3.
Матрицу (12.3) называют производящей, или порождающей, матрицей кода (7,4), содержащего семь элементов, из которых четыре информационных. Обычно матрицу обозначают буквой G с индексом, указывающим, к какому коду она относится (в нашем случае G(7,4)). Производящая матрица состоит из двух матриц — единичной (размерности k• k) и С(r,k) , содержащей r столбцов и kстрок. Суммируя в различном сочетании строки матрицы (12.3), получаем все (кроме нулевой) комбинации корректирующего кода с do= 3.
|
|
Единицы, расположенные на местах, соответствующих информационным элементам матрицы Н(7,4), указывают на то, какие информационные элементы должны участвовать в формировании проверочного элемента. Единица на месте, соответствующем проверочному элементу, указывает, какой проверочный элемент получается при суммировании по модулю два

Комбинация b3b2b1называется синдромом (проверочным вектором). Равенство нулю всех элементов синдрома указывает на отсутствие ошибок, или на то, что кодовая комбинация принята с ошибками, которые превратили ее в другую разрешенную. Последнее событие имеет существенно меньшую вероятность, чем первое.
Вид ненулевого синдрома определяется характером ошибок в кодовой комбинации. В нашем случае вид синдрома зависит от местоположения одиночной ошибки. В табл. 12.2 отражено соответствие между местоположением одиночной ошибки для кода, заданного матрицей (12.3), и видом синдрома.
Таким образом, зная вид синдрома, можно определить место, где произошла ошибка, и исправить принятый элемент на противоположный.
|
|
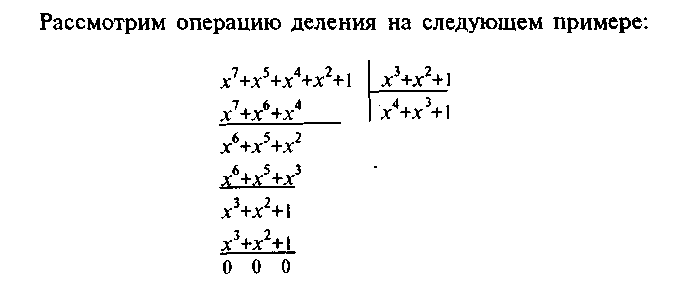
Деление выполняется как обычно, только вычитание заменяется суммированием по модулю два.
Разрешенные комбинации циклического кода обладают двумя очень важными отличительными признаками: циклический сдвиг разрешенной комбинации тоже приводит к разрешенной кодовой комбинации. Все разрешенные кодовые комбинации делятся без остатка на полином Р(х), называемый образующим. Эти свойства используются при построении циклических кодов, кодирующих и декодирующих устройств, а также при обнаружении и исправлении ошибок.
Найдем алгоритмы построения циклического
кода, удовлетворяющего перечисленным выше условиям. Задан полином ![]() , определяющий корректирующую способность
кода, и задан исходный простой код, который требуется преобразовать в
корректирующий циклический.
, определяющий корректирующую способность
кода, и задан исходный простой код, который требуется преобразовать в
корректирующий циклический.
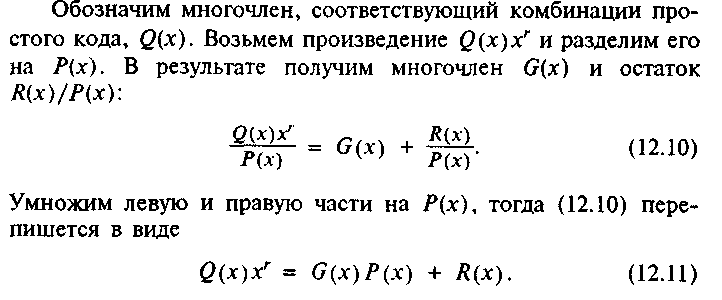
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.